System of linear differential equations
Given System of linear differential equations with constant coefficient:
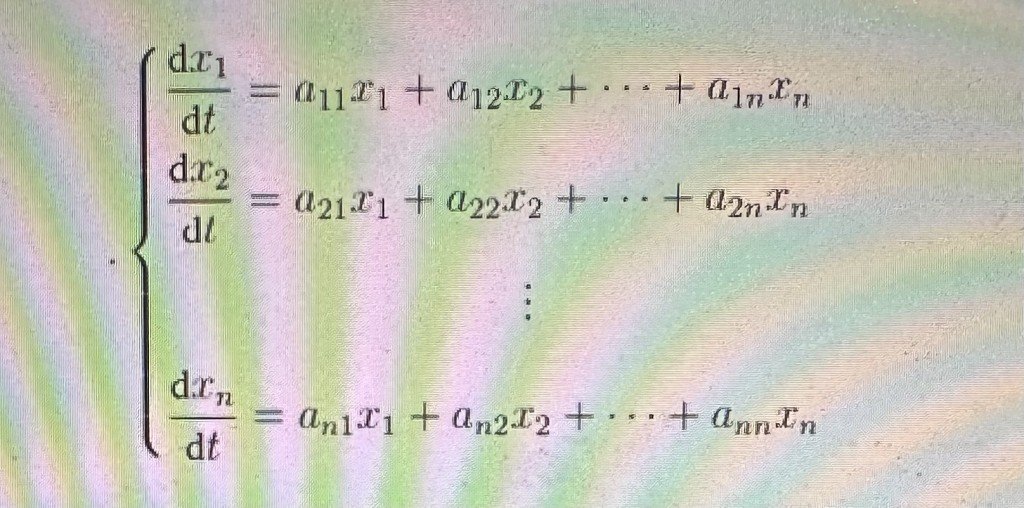
The matrix coefficient :
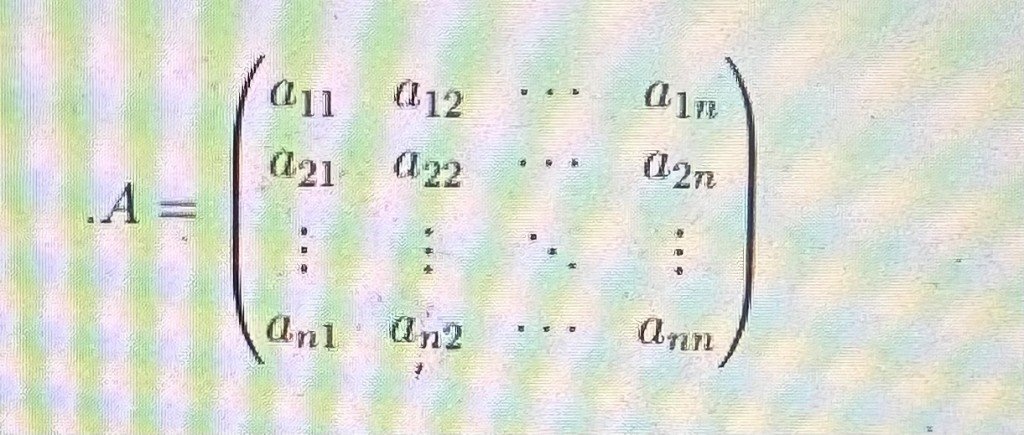
And also given that the vector :
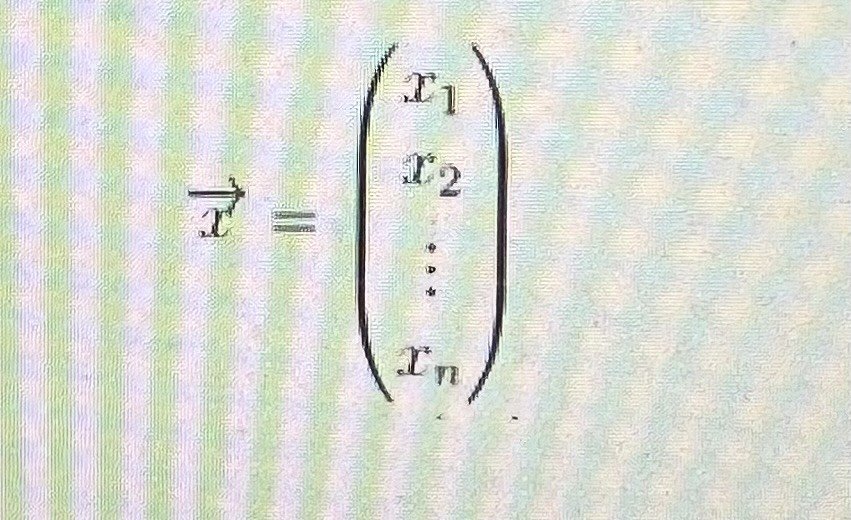
Is a solution to the system.
1.Show that x1(t),x2(t),...,xn(t) are differetiable from every order in interval I and also that:
\[\frac{d^k \mathbf{x}(t)}{dt^k} = \mathbf{A}^k \mathbf{x}(t),\]
2.Show that there Is System of linear differential equations with constant coefficient from order n such that
x1(t),..,xn(t) are a solution. Hint: Kylie Hamilton theorem
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
1 Attachment
Martin
-
I understand why we can differentiate one time, but what is the justification for second, third, and go on?
-
It's by mathematical induction. The step from n-1 to n allows to go from 2 to 3 to 4 to ... To be rigorous you only need the step from 1 to 2 (the base case) and from n-1 to n (the induction step).
-
- answered
- 189 views
- $15.00
Related Questions
- Find a formula for the vector hyperbolic problem
- ODEs - Stability
- What is the transfer function of this system of differential equations?
- Conservative system ODE
- Solving a system of linear ODE with complex eigenvalues
- Solve $Lx = b$ for $x$ when $b = (1, 1, 2)^T$.
- Long time behavior of solutions of an autonomous differential equation
- Ordinary Differential Equations Integrating Factors Assignment
