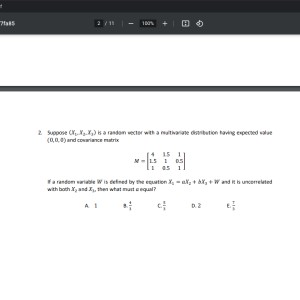
Question dealing with random vector and covariance matrix, also with an equation of random variables(file below)
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
 Mathe
Mathe
3.7K
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1506 views
- $30.00
Related Questions
- Poisson process question
- Bivariate Normality questions
- Product of Numbers from a Log Normal Distribution
-
Poker Outcomes and Variance: Calculating Likelihood of an Observed Outcome
- X is number of (fair) coin flips needed to land m heads OR m tails. m is arbitrary natural number. Delfine CDF of X. (in It's simplest form)
- foundations in probability
- Slot Machine Probability
- Pdf/cdf Probability