Need help with integrals (Urgent!)
Let X and Y be two random variables with joint density function
1. Check that f is a joint probability density function.
2. Calculate the following probabilities:
(a) P(X ≥ 1/2 )
(b) P(X ≤ 1/2,Y ≤ 1/2).
3. Determine the marginal density of X and that of Y.
4. Determine the conditional densities of X and Y.
5. Calculate the conditional expectations of X and Y.
Sasha
16
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
2 Attachments
Kav10
1.9K
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 463 views
- $20.00
Related Questions
- Find a number for 𝛼 so f(x) is a valid probability density function
- Application of Integrals
- Second order directional derivative
- Insurance question involving net premium
- A bag contains 3 red jewels and 7 black jewels. You randomly draw the jewels out one by one without replacement. What is the probability that the last red jewel was the 8th one withdrawn?
- Conditional mean and variance for joint PDF
- What is the integral of (x^2-8)/(x+3)dx
- Optimal Control - Calculus of Variations
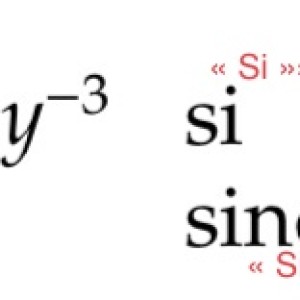
What is the formula for f?
I uploaded the file. Thank you !
Is it possible to make a step by step solution so k can understand the solving process
Kav10, I have made a mistake setting the deadline. The deadline is actually in 10h hours. Is it still possible for you ?
Let me see what I can do. I am out and will be home in ~5 hours. Can you please give me an exact deadline? Like is it 7 am Eastern Time?
10-11AM Eastern Time
OK. I’ll try to send late tonight!