Spot my mistake and fix it so that it matches with the correct answer. The problem is calculus based.
The problem is: what is the integral of [1/root(x^2-9)]dx? The image is posted below. The answer is supposed to be ln |(x+root(x^2-9)| +C. Obviously I got pretty close but I can't seem how to eliminate the 3 in the solution. I'm genuinely stuck at this problem. I also apologize that I set the time to less then an hour but I really need to get this done to tonight.
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
1 Attachment
Erdos
4.8K
-
Wow, I never saw it that way. Thanks!
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1490 views
- $2.00
Related Questions
- highschool class help
- Use the equation to show the maximum, minimum, and minimum in the future.
- Parametric, Polar, and Vector-Valued Equations for Kav10
- Create a rational function, g(x) that has the following properties.
- Equations of Motion and Partial Fractions
- 3 Multi-step response questions
- Integration and Accumulation of Change
- Determine values of a,b and c so that f(0)=0 and f(8)=0 and f'(2)= 16
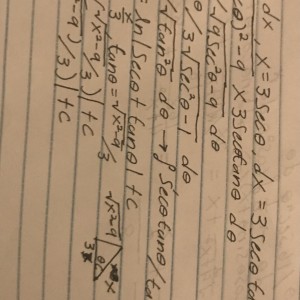
Sorry the answer is supposed to be ln |root(x^2-9) + x| +C