What is the integral of (x^2-8)/(x+3)dx
What is the integral of [(x^2-8)/(x+3)]dx? I've been stuck on this problem for a couple hours. I know it's something simple that is completely going over my head, but I really need it done by tonight. I already know what the answer is. Im not looking for the answer I'm looking how to solve the problem step by step. The answer to the problem is (x^2)/2 - 3x + ln|x+3| + C. The problem is supposed to be solved by trigonometric substitutions. I posted an image to show how the problem is supposed to look like. This is my failed attempt. Sorry if it looks messy, I wrote it not expecting to show anyone. Thanks
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
1 Attachment
Erdos
4.8K
-
Well.. guess you did it
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1858 views
- $2.00
Related Questions
- Find and simplify quotient
- [Help Application of Integration]Question
- Connected rates of change calculus.
- Compute $\lim\limits_{x \rightarrow 0} \frac{1-\frac{1}{2}x^2-\cos(\frac{x}{1-x^2})}{x^4}$
- Explain proof of directional derivative
- Under the hood of Hard Margin SVM
- Finding absolute and relative extrema given an equation.
- Find $\int\frac{dx}{2x^2-2x+1}$
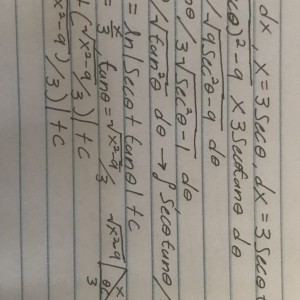
Sorry I posted the wrong problem. The problem is actually the integral of [1/((4+x^2)^2)]dx
Oh and it looks like I posted the wrong answer to the problem as well. Sorry my brain is feeling overwhelmed recently with all the math work. The answer to the problem is actually 1/16 arctan(x/2) + (x(4+x^2))/8 + C