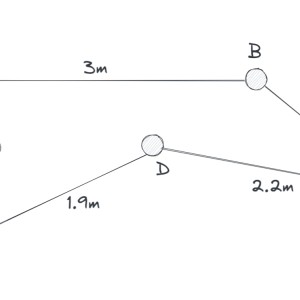
How to recalculate 2D polygon side lengths when tilt is applied in 3D space?
So I have a polygon in 2D space (see image https://i.stack.imgur.com/lSEWn.png). Let's say that I have correctly calculated all of the lengths of all sides of the polygon. Now, I want to apply a 30deg tilt to this polygon in 3D space, so that the points (A, F, E, D, B) are "taller" than the point (C). In other words, the tilt starts from the point C and goes "upwards".
I am not too sure how to express this in mathematical terms, but the 30deg angle should start at the point C, which will make the other points progressively "taller" than the point C, and the point furthest away from C will be the "tallest". Note that the points should remain fixed in 2D space, they should only move up in 3D space.
My question is: given this 2D polygon and a tilt to be applied in 3D space, how are the sides (A,B), (B,C), (D,C), (E,D), (F, E) and (A,F) affected? I know that they will become lengthier because in 3D space the depth will affect the length, but by how much?
Also, which branch of mathematics does this kind of problem belong to? What kind of material should I read up on in order to be able to better recognize and formulate problems of this nature?
 Nkalpak
Nkalpak
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
-
Thank you very much! How would you generalize the A'B' formula to work with angles between 0-90 degrees? If I understand correctly, the formula outlined above will only work for angles of 30 degrees.
- answered
- 1851 views
- $9.84
Related Questions
- Vector-valued functions and Jacobian matrix
- Improper integral
- A telephone line hanging between two poles.
- Find $\lim_{x \rightarrow} x^2 \sin(1/x) $. Cite theorems used and show all work
- Calculate the following, if it exists: $\int_{0}^{1} x^a(lnx)^mdx$ , where $a > -1$ and $m$ is a nonnegative integer.
- Studying the graph of this function
- Show that $\sum_{n=1}^{\infty} \frac{\sin n}{n}$ is convergent
- Characterizing the Tangent and Normal Bundles - Submanifolds in Banach Spaces and Their Classifications