$Quick question regarding Analytical Applications of Differentiation$

Question

$Quick question regarding Analytical Applications of Differentiation$

I am still a student, I am thrilled in learning, so please be throughly :)

Question pictures bellow:

The following quick question regarding: Analytical Applications of Differentiation

References:
https://teachingcalculus.com/2021/10/12/unit-5-analytical-applications-of-differentiation-2/
https://calculus.flippedmath.com/unit-5.html

Transcript:

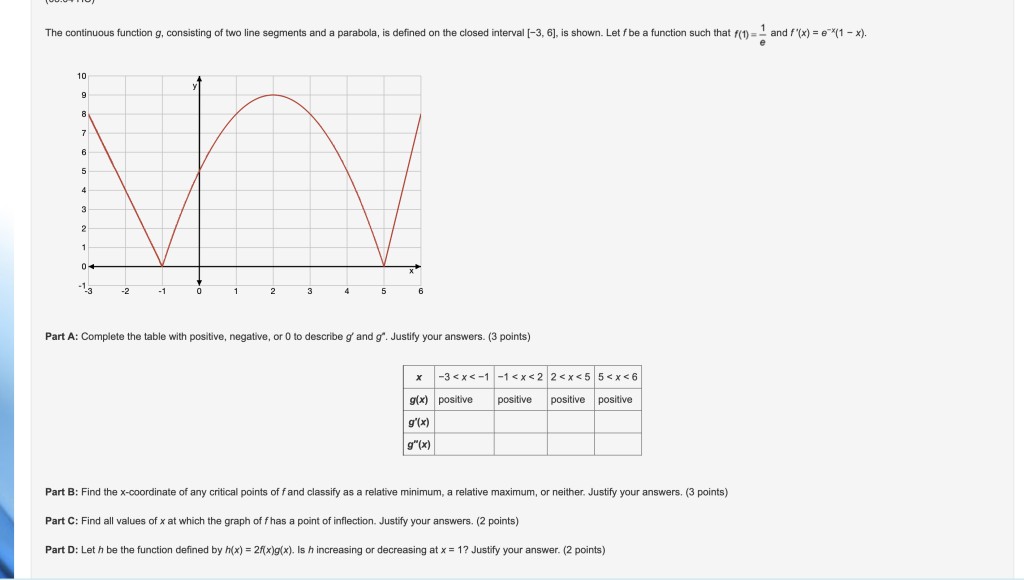
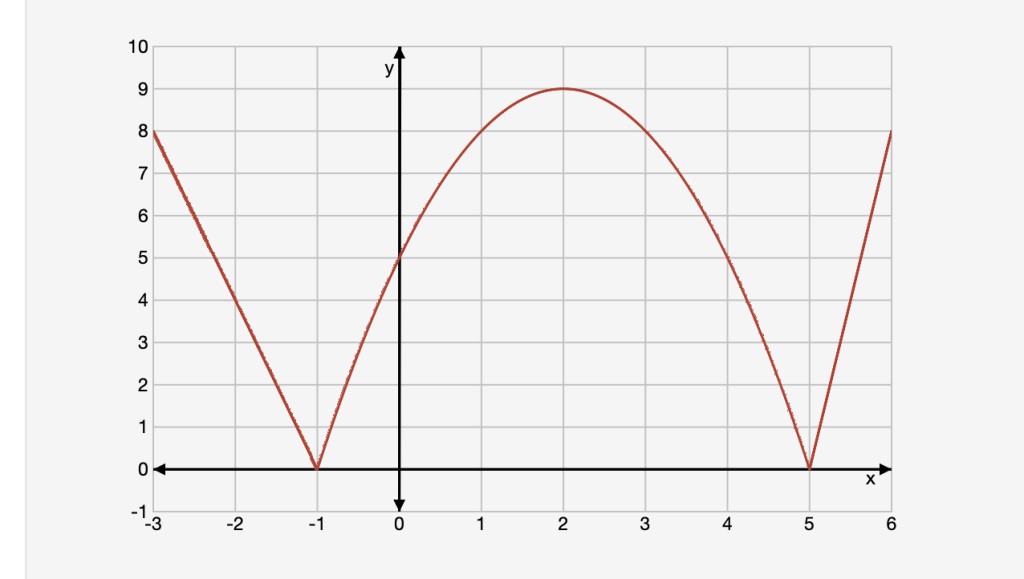
The continuous function g, consisting of two line segments and a parabola, is defined on the closed interval [−3, 6], is shown. Let f be a function such that f(1) = 1/e and f ′(x) = e^(−x) (1 − x).

Part A: Complete the table with positive, negative, or 0 to describe g′ and g″. Justify your answers. (3 points)

Table attached

Part B: Find the x-coordinate of any critical points of f and classify as a relative minimum, a relative maximum, or neither. Justify your answers. (3 points)

Part C: Find all values of x at which the graph of f has a point of inflection. Justify your answers. (2 points)

Part D: Let h be the function defined by h(x) = 2f(x)g(x). Is h increasing or decreasing at x = 1? Justify your answer. (2 points)

Calculus Derivatives Complex Numbers

Nicolas Santana

300

Matchmaticians Quick question regarding Analytical Applications of Differentiation File #1

File #1 (png)

Matchmaticians Quick question regarding Analytical Applications of Differentiation File #2

File #2 (png)

Report

Savionf

0

Low bounty for a multiple part question.
Nicolas Santana

0

@blue can you please answer it, we don't turn things in near the deadline. Thanks

Answer

The answer is accepted.

Join Matchmaticians Affiliate Marketing Program to earn up to a 50% commission on every question that your affiliated users ask or answer.

Nicolas Santana

0

@blue can you please answer it, we don't turn things in near the deadline. Thanks

Answer 1

Answers can only be viewed under the following conditions:

The questioner was satisfied with and accepted the answer, or
The answer was evaluated as being 100% correct by the judge.

View the answer

When $-3 < x < -1$, the function is above the $x$-axis, and decreasing linearly. Thus $g(x) > 0$, $g'(x) < 0$, and $g''(x) = 0$.

When $-1 < x < 2$, the function is above the $x$-axis, and increasing more and more slowly (it is concave down). Thus $g(x) > 0$, $g'(x) > 0$, and $g''(x) < 0$.

When $2 < x < 5$, the function is above the $x$-axis, and decreasing more and more quickly (it is concave down). Thus $g(x) > 0$, $g'(x) < 0$, and $g''(x) < 0$.

When $5 < x < 6$, the function is above the $x$-axis, and increasing linearly. Thus $g(x) > 0$, $g'(x) > 0$, and $g''(x) = 0$.

$x$	$-3 < x < -1$	$-1 < x < 2$	$2 < x < 5$	$5 < x < 6$
$g(x)$	positive	positive	positive	positive
$g'(x)$	negative	positive	negative	positive
$g''(x)$	zero	negative	negative	zero

The critical points of $f$ occur when $f'(x) = 0$. This means $e^{-x}(1-x) = 0$. Multiplying both sides by $e^x$ gives that $x = 1$. To determine if this is a relative maximum or minimum, we look at the second derivative (product rule) to get $f''(x) = -e^{-x}(1-x) -e^{-x}$. At $x = 1$ we get $f''(1) = e^{-1}(1-1) - e^{-1} = -1/e < 0$. Thus this is a relative maximum.

$f$ has an inflection point whenever the second derivative changes sign. We have $f''(x) = -e^{-x}(1-x) -e^{x} = e^{-x}(x-2)$. This changes sign at $x=2$, since $e^{-x}$ is always positive.

We need to take the derivative of $h$. It is $h'(1) = 2(f'(1)g(1) + f(1)g'(1))$. Using the table, we have that $g'(1) > 0$. Furthermore, we already know that $f(1) = 1/e > 0$ and $f'(1) = 0$. That means $h'(1) = 2f(1)g'(1) > 0$. So the function is increasing at $x=1$.

Blue

166

$Quick question regarding Analytical Applications of Differentiation$

Answer

Related Questions

Search