Induced and restricted representation

I assume that by "permutation representation" you mean $S_3$ acting on $\mathbb{C}^3$ by permuting the basis vectors.

The permutation representation on $S_n$ is the direct sum of the representationss indexed by the partitions $(n)$ and $(n-1,1)$. Now, there is a combinatorial rule for computing the induced representation: thinking of the partitions as corresponding to their Young diagrams, inducing the representation corresponding to a partition gives the sum over all partitions obtained by adding one box to the given partition. When you do this you get the direct sum \[ Ind^{S_{n+1}}_{S_n} ((n) \oplus (n−1,1))=(n+1) \oplus (n,1) \oplus (n,1) \oplus (n−1,2) \oplus (n−1,1,1). \] Similarly, restricting a representation of $S_{n+1}$ to $S_n$ we get the sum over all partitions obtained by removing one box from the given partition, so we get \[ Res_{S_n}^{S_{n+1}} Ind^{S_{n+1}}_{S_n} ((n) \oplus (n−1,1)) = (n) \oplus ((n) \oplus (n-1, 1)) \oplus ((n) \oplus (n-1, 1)) \\ \oplus ((n-1,1) \oplus (n-2, 2)) \oplus ((n-1,1) \oplus (n-2, 1, 1)). \] Note that, for $n=3$, $(n-2, 2)$ is not a partition and so that should be removed.

Note that these two rules are equivalent by Frobenius reciprocity, and both can be easily derived by definition of Specth module. https://en.wikipedia.org/wiki/Specht_module

Let me know if this is satisfying or if the exercise was meant to be done with elementary tools.

Long answer (incomplete atm - will edit later):

Let's take as $S_4/S_3$ coset representatives the elements $g_i = (i,4)$ for $1 \leq i \leq 4$. The representation $Ind_{S_3}^{S_4}(V)$ acts on the space \[ W = \bigoplus_{i=1}^4 g_i V. \] Let us have $V = \langle e_1, e_2, e_3 \rangle$ with $\sigma(e_j) = e_{\sigma(j)}$ for $\sigma \in S_3$, and call $e_j^i$ the copy of $e_j$ in $g_i V$. Let $\sigma \in S_4$. We have $\sigma g_i = g_{\sigma(i)} \overline{\sigma}$ for some $\overline{\sigma} \in S_3$ (seen as an element of $S_4$ that fixes $4$. Indeed, $\sigma g_i(4) = \sigma(i)$ and $g_{\sigma(i)} \overline{\sigma}(4) = g_{\sigma(i)}(4) = \sigma(i)$, so the computation checks out. It follows that, is $\sigma$ has no fixed points, it permutes the subspaces and so the trace is $0$.

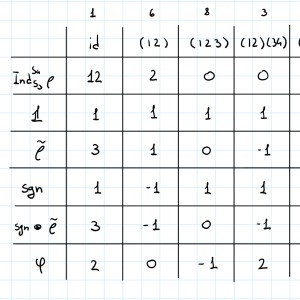
We want to compute the character now. We have $5$ conjugacy classes in $S_4$, given by the partitions $(4)$, $(3,1)$, $(2,2)$, $(2,1,1)$, $(1,1,1,1)$. We immediately have that $\chi_W(4) = \chi_W(2,2) = 0$ as they do not have fixed points. Then, $\chi_W(3,1) = 0$ because it fixes one subspace (say $g_i V$), but then permutes the basis of that subspace $e_1^i, e_2^i, e_3^i$ keeping no fixed points. Next, $\chi_W(2,1,1) = 2$ as it fixes two subspaces, and one basis vector within each subspace. Finally, $\chi_W(1,1,1,1) = 12$ because the character of the identity always gives the dimension of the space.

We need the character table of $S_4$ now (see attachment - it can be computed by starting from the trivial representation and $\tilde{\rho}$ (the permutation rep minus the trivial), then tensoring with the sign, and then filling the rest by orthogonality relations.

We now want to decompose $Ind_{S_3}^{S_4}(V)$ in irreducibles. For sure, the sum of all the basis vectors is fixed by any permutation, so that gives an invariant subspace of dimension one, which corresponds to the partition $(4)$ (the trivial representation). Next, the space generated by the vectors $e^i_1 + e^i_2 + e^i_3$ for $1 \leq i \leq 4$, on which $S_4$ acts by permuting the upper indices $i$; this is the standard permutation representation, so, the trivial representation is a subrepresentation, and the orthogonal complement forms an irreducible representation associated to the partition $(3,1)$, (so, $\rho$).

Now, since $\chi_{Ind_{S_3}^{S_4}(V)}((123)) = 0$, and the only representation whose character has a minus sign in that column is $\phi$, we need to include at least one copy of that. So far, summing the characters of our three irreducibles gives the values $(6, 2, 0, 0, 0)$, so we need two more representations whose global character gives $(6,0,0,0,0)$. Looking at the values on $(12)(34)$, we immediately see that we cannot include another copy of $\phi$, as otherwise we would need two more $3$-dimensional representations to compensate and there's not enough space left. But if we can't include $\phi$, then we can't include the trivial or the sign either, because of the values on $(123)$. It is now immediate that we are left with a copy of $\tilde{\rho}$ and a copy of $\tilde{\rho} \otimes sgn$: the total dimension is $12$, so we have our decomposition. The characters check out. In the end,

\[ Ind^{S_{n+1}}_{S_n} (V)= 1_4 \oplus \tilde{\rho} \oplus \tilde{\rho} \oplus \phi \oplus (\tilde{\rho} \otimes sgn). \]
For the restriction, we can use Frobenius reciprocity. We have three irreducible representations of $S_3$, namely the trivial, the sign, and the permutation minus trivial (let us call them $1_3, sgn_3, \rho_3)$.

Now, using pretty much the same argument as above, $Ind_{S_3}^{S_4} 1_3$ gives the permutation representation of $S_4$, which decomposes as $1_4 \oplus \tilde{\rho}$.

Next, $Ind_{S_3}^{S_4} sgn_3$ gives the signed permutation representation of $S_4$ (the same, but tensoring with the sign), which decomposes as $sgn_4 \oplus (\tilde{\rho} \otimes sgn_4)$.

Finally, the induced of the standard representation $Ind_{S_3}^{S_4} \rho_3$ decomposes as the complement of the induced of the trivial in $Ind_{S_3}^{S_4} V$, so as $\tilde{\rho} \oplus \phi \oplus (\tilde{\rho} \otimes sgn_4)$.

Using the Frobenius reciprocity, $1_4$ restricts to $1_3$ (because $1_4$ appears once in the induced from $1_3$ and nowhere else, then $1_3$ appears with the same multiplicity in the restriction of $1_4$), $\tilde{\rho}$ restricts as $1_3 \oplus \rho$ (same reason - and the analogous when tensoring with the sign), and $\phi$ restricts as $\rho$ (again, same reason). Putting everything together, we have \[ Res_{S_n}^{S_{n+1}} Ind^{S_{n+1}}_{S_n} (V) = 1_3 \oplus (1_3 \oplus \rho) \oplus (1_3 \oplus \rho) \oplus (sgn_3 \oplus \rho) \oplus \rho.  \]