How do we define a measure of discontinuity which gives what I want?
#1. Motivation:
Suppose $d$ is the dimension of the $d$-dimensional Hausdorff measure, $\dim_{\text{H}}(\cdot)$ is the Hausdorff dimension and $\mathcal{H}^{\dim_{\text{H}}(\cdot)}(\cdot)$ is the Hausdorff measure in its dimension on the Borel $\sigma$-algebra. Moreover, $f:X\to Y$ is a function from $X\subseteq\mathbb{R}$ to $Y\subseteq\mathbb{R}$, and $X_1\subseteq\mathbb{R}$ is an arbitrary set.
We want to define a measure of discontinuity of $f$ between zero and infinity, where the more disconnected the graph of $f$ on $X_1$, the larger the measure. For instance, when $f$ is continuous on $X\cap X_1$ the measure should be zero and when $f$ is "extremely disconnected" on $(X\cap X_1)\times Y$ the measure should be positive infinity.
In topology, when the function $f$ is continuous, its restriction to a set dense in $X$ is continuous and must have zero measure of discontinuity: the domain $X'=X\cap X_1$ of the restriction $f|_{X'}$ has a Hausdorff dimension less than or equal to the dimension of $X$. Hence, when $\dim_{\text{H}}(X')<\text{dim}_{\text{H}}(X)$, the measure of discontinuity should be zero. In contrast, when $\dim_{\text{H}}(X_1)>\text{dim}_{\text{H}}(X)$, the measure should be positive infinity: e.g., the function $f$ is not continuous on the domain of its extension $F:X_1\supset X\to Y$ since $X_1\setminus X$ has a positive Hausdorff measure in the dimension of $X_1$. Thus, we are left with $\dim_\text{H}(X\cap X_1)=\dim_{\text{H}}(X)$, where the measure can be any number in $[0,\infty]$ based on intuitive reasoning.
Note, the definition of continuity is:
Definition. Suppose $X\subseteq\mathbb{R}$ and $Y\subseteq\mathbb{R}$ are arbitrary sets. The continuity of $f:X\to Y$ at $x_0\in X$ means that for every $\epsilon>0$, there exists a $\delta>0$ such that for all $x\in X\setminus\{x_0\}$ $$|x-x_0|<\delta \quad \text{implies} \quad |f(x)-f(x_0)|<\epsilon$$ Hence, $f$ is continuous on the arbitrary set $X_1\subseteq\mathbb{R}$, such that:
• $\dim_{\text{H}}(\cdot)$ is the Hausdorff dimension
• $\mathcal{H}^{\dim_{\text{H}}(\cdot)}(\cdot)$ is the Hausdorff measure in its dimension on the Borel $\sigma$-algebra
whenever:
$$C_\mathcal{M}:=\mathcal{H}^{\dim_{\text{H}}(X_1)}(X_1\setminus X)=0$$ Question: Is there a measure of discontinuity which satisfies the criteria below? (My attempt to answer this question is on Section #3.) If the attempt is correct (i.e., see Sec. 3.3 of File #3 for evidence), it's still extremely long. Is there a easier measure that satisfies all the criteria?
#2. Criteria for the Measure:
Suppose $X\subseteq\mathbb{R}$ and $Y\subseteq\mathbb{R}$ are arbitrary sets, where $f:X\to Y$ is a function. Moreover, $\dim_{\text{H}}(\cdot)$ is the Hausdorff dimension and $\mathcal{H}^{\dim_{\text{H}}(\cdot)}(\cdot)$ is the Hausdorff measure in its dimension on the Borel $\sigma$-algebra. Note, $X_1\subseteq\mathbb{R}$ is an arbitrary set and $X'=X\cap X_1$.
(1) The measure of discontinuity must range between zero and positive infinity
(2) When $X\cap X_1$ is empty, the measure is zero regardless of $\dim_{\text{H}}(X\cap X_1)$ and $\dim_{\text{H}}(X)$
(3) When $f$ is discrete but $X\cap X_1$ is non-empty, the measure is $+\infty$ regardless of $\dim_{\text{H}}(X)$ and $\dim_{\text{H}}(X\cap X_1)$
(4) When the function is continuous on $X_1$, the measure is zero.
(5) When $f$ is "hyper-discontinuous", the measure is positive infinity.
(6) When the closure of the graph of $f$ can be split into a minimum of $n$ function continuous on a positive measure subset of $X_1$ where any vertical line, whose $x$-intercepts are elements of $X$, intersects the limit points $m$ to $n$ times ($m<n$):
(6.1) If $\dim_{\text{H}}(X\cap X_1)<\dim_{\text{H}}(X)$, the measure is a number between $m-1$ and $n-1$ where:
(6.1.1) the variable $\mathfrak{c}$ is the number of the times the vertical line intersects the closure with respect to its $x$-intercept
(6.1.2) $\limsup_{j\to\infty}\mathbf{X}_j'=\liminf_{j\to\infty}\mathbf{X}_j'=X'$ (i.e., the set theoretic limit) such that $0<\mathcal{H}^{\dim_{\text{H}}(X')}(\mathbf{X}_{j}')<+\infty$ for all $j\in\mathbb{N}$
(6.1.3) the arbitrary set ${\overline{X_\mathfrak{c}}}\subseteq X\cap X_1$ has the largest Hausdorff measure in the Hausdorff dimension of $X\cap X_1$, such that the vertical line for all $x\in \overline{X_{\mathfrak{c}}}$ intersects the closure $\mathfrak{c}$ times ($m\le \mathfrak{c}\le n$)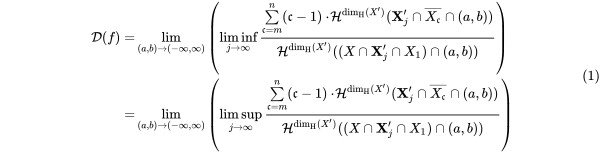 (6.2) If $\dim_{\text{H}}(X\cap X_1)=\dim_{\text{H}}(X)$, and corresponds to the weighted average $\mathcal{D}(f)$
(6.2) If $\dim_{\text{H}}(X\cap X_1)=\dim_{\text{H}}(X)$, and corresponds to the weighted average $\mathcal{D}(f)$
(6.3) If $\dim_{\text{H}}(X_1)>\dim_{\text{H}}(X)$, the measure is positive infinity
(7) When the graph of $f$ is dense in the closure of $X'\times Y$, where we remove the subset of the graph of $f$ with zero Hausdorff measure in its dimension and left with the minimum of $n$ functions continuous on a positive measure subset of $X_1$:
(7.1) If $\dim_{\text{H}}(X\cap X_1)<\dim_{\text{H}}(X)$, the measure is zero
(7.2) If $\dim_{\text{H}}(X\cap X_1)=\dim_{\text{H}}(X)$, the measure is $n-1$
(7.3) If $\dim_{\text{H}}(X_1)>\dim_{\text{H}}(X)$, the measure is positive infinity
(8) When the graph of $f$ is dense in the closure of $X'\times Y$, where the graph has zero Hausdorff measure in its dimension, the measure is positive infinity.
#3. Attempt To Define A Measure:
You can ignore this section, though parts of this can be used for a better answer. (I will post a paper with examples showing my measure satisfies the criteria in Section #2.)
Suppose:
• $X\subseteq \mathbb{R}$, $Y\subseteq\mathbb{R}$, and $Y\subseteq\mathbb{R}$ are arbitrary sets
• $f:X\to Y$ is a function
• $d\in[0,1]$
• $\dim_{\text{H}}(\cdot)$ or $d^{\prime}(\cdot)$ is the Hausdorff dimension
• $\mathcal{H}^{\dim_{\text{H}}(\cdot)}(\cdot)$ is the Hausdorff measure in its dimension on the Borel $\sigma$-algebra
• $d_1=\dim_{\text{H}}(X_1)$
• $X'=X\cap X_1$
• $X'\cap(a,b)=X'(a,b)$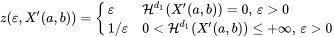 • $\limsup_{j\to\infty}X_{j}(a,b)=\liminf_{j\to\infty}X_j(a,b)=X'(a,b)$ such that $0<\mathcal{H}^{d_1}(X_{j}(a,b))<+\infty$ for all $j\in\mathbb{N}$
• $\limsup_{j\to\infty}X_{j}(a,b)=\liminf_{j\to\infty}X_j(a,b)=X'(a,b)$ such that $0<\mathcal{H}^{d_1}(X_{j}(a,b))<+\infty$ for all $j\in\mathbb{N}$
• $\mathbf{R}(X_j(a,b))=\inf\{\mathcal{H}^{\dim_{\text{H}}(\text{Range}(f))}(R): R\subseteq Y, \mathcal{H}^{d_1}(f^{-1}[R]\cap X_j(a,b))=\mathcal{H}^{d_1}(X_j(a,b))\}$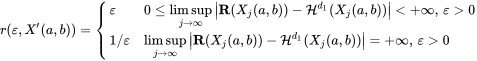 • $G(X'(a,b))$ is the graph of $\left.f\right|_{X'(a,b)}$
• $G(X'(a,b))$ is the graph of $\left.f\right|_{X'(a,b)}$
•$\limsup_{j\to\infty}\mathsf{G}_{j}(X(a,b))=\liminf_{j\to\infty}\mathsf{G}_j(X(a,b))=G(X'(a,b))$, where for all $j\in\mathbb{N}$, $0<\mathcal{H}^{d_1}(\mathsf{G}_{j}(X(a,b)))<+\infty$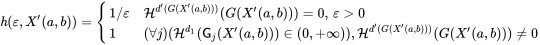 • $\mathcal{P}_{k}(d,G(X'(a,b)))=\left\{\mathbf{G}\subseteq G(X(a,b)):\mathcal{H}^{d_1}(\mathbf{G})=k\right\}$
• $\mathcal{P}_{k}(d,G(X'(a,b)))=\left\{\mathbf{G}\subseteq G(X(a,b)):\mathcal{H}^{d_1}(\mathbf{G})=k\right\}$
• $G_k(d,X'(a,b))\in\mathcal{P}_{k}(d,G(X'(a,b)))$
• $\mathbb{G}_{0}(d,X'(a,b))$ is all limit points of $G(X'(a,b))\setminus G_0(d,X'(a,b))$
• $\#|\cdot|$ is the counting measure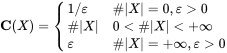 • $\ell(X'(a,b))\subset \mathbb{R}^2$ is an arbitrary, vertical line whose $x$-intercept is an element of $X'(a,b)$
• $\ell(X'(a,b))\subset \mathbb{R}^2$ is an arbitrary, vertical line whose $x$-intercept is an element of $X'(a,b)$
• $\mathtt{C}_0(d,\ell,X'(a,b))=\inf\limits_{{G}_{0}(d,X'(a,b))\in\mathcal{P}_{0}(d,X(a,b))}\mathbf{C}(\mathbb{G}_{0}(d,X'(a,b))\cap\ell(X'(a,b)))$
Then, when defining:
• $\limsup_{j\to\infty}\mathbf{X}_{j}(a,b)=\liminf_{j\to\infty}\mathbf{X}_j(a,b)=X'(a,b)$ such that $0<\mathcal{H}^{\dim_{\text{H}}(X')}(\mathbf{X}_{j}(a,b))<+\infty$ for all $j\in\mathbb{N}$
• $\mathbf{M}(\varepsilon,d,\ell,X'(a,b))=z(\varepsilon,X'(a,b))\cdot r(\varepsilon,X'(a,b))\cdot \mathtt{C}_{0}(d,\ell,X'(a,b))\cdot\mathit{h}(\varepsilon,X'(a,b))$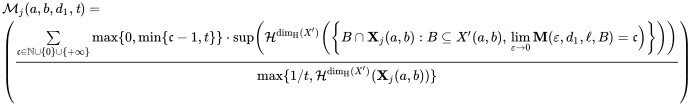 $\mathcal{D}_{d_1}$ is the $d$-dimensional measure of discontinuity (when the limit exists)$$\mathcal{D}_{d_1}=\lim\limits_{(a,b)\to(-\infty,\infty)}\left(\lim_{t\to\infty}\big(\liminf_{j\to\infty}\mathcal{M}_j(a,b,d,t)\big)\right)\\ \quad\;\quad=\lim\limits_{(a,b)\to(-\infty,\infty)}\left(\lim_{t\to\infty}\big(\limsup_{j\to\infty}\mathcal{M}_j(a,b,d,t)\big)\right)$$
$\mathcal{D}_{d_1}$ is the $d$-dimensional measure of discontinuity (when the limit exists)$$\mathcal{D}_{d_1}=\lim\limits_{(a,b)\to(-\infty,\infty)}\left(\lim_{t\to\infty}\big(\liminf_{j\to\infty}\mathcal{M}_j(a,b,d,t)\big)\right)\\ \quad\;\quad=\lim\limits_{(a,b)\to(-\infty,\infty)}\left(\lim_{t\to\infty}\big(\limsup_{j\to\infty}\mathcal{M}_j(a,b,d,t)\big)\right)$$
Suppose $d$ is the dimension of the $d$-dimensional Hausdorff measure, $\dim_{\text{H}}(\cdot)$ is the Hausdorff dimension and $\mathcal{H}^{\dim_{\text{H}}(\cdot)}(\cdot)$ is the Hausdorff measure in its dimension on the Borel $\sigma$-algebra. Moreover, $f:X\to Y$ is a function from $X\subseteq\mathbb{R}$ to $Y\subseteq\mathbb{R}$, and $X_1\subseteq\mathbb{R}$ is an arbitrary set.
We want to define a measure of discontinuity of $f$ between zero and infinity, where the more disconnected the graph of $f$ on $X_1$, the larger the measure. For instance, when $f$ is continuous on $X\cap X_1$ the measure should be zero and when $f$ is "extremely disconnected" on $(X\cap X_1)\times Y$ the measure should be positive infinity.
In topology, when the function $f$ is continuous, its restriction to a set dense in $X$ is continuous and must have zero measure of discontinuity: the domain $X'=X\cap X_1$ of the restriction $f|_{X'}$ has a Hausdorff dimension less than or equal to the dimension of $X$. Hence, when $\dim_{\text{H}}(X')<\text{dim}_{\text{H}}(X)$, the measure of discontinuity should be zero. In contrast, when $\dim_{\text{H}}(X_1)>\text{dim}_{\text{H}}(X)$, the measure should be positive infinity: e.g., the function $f$ is not continuous on the domain of its extension $F:X_1\supset X\to Y$ since $X_1\setminus X$ has a positive Hausdorff measure in the dimension of $X_1$. Thus, we are left with $\dim_\text{H}(X\cap X_1)=\dim_{\text{H}}(X)$, where the measure can be any number in $[0,\infty]$ based on intuitive reasoning.
Note, the definition of continuity is:
Definition. Suppose $X\subseteq\mathbb{R}$ and $Y\subseteq\mathbb{R}$ are arbitrary sets. The continuity of $f:X\to Y$ at $x_0\in X$ means that for every $\epsilon>0$, there exists a $\delta>0$ such that for all $x\in X\setminus\{x_0\}$ $$|x-x_0|<\delta \quad \text{implies} \quad |f(x)-f(x_0)|<\epsilon$$ Hence, $f$ is continuous on the arbitrary set $X_1\subseteq\mathbb{R}$, such that:
• $\dim_{\text{H}}(\cdot)$ is the Hausdorff dimension
• $\mathcal{H}^{\dim_{\text{H}}(\cdot)}(\cdot)$ is the Hausdorff measure in its dimension on the Borel $\sigma$-algebra
whenever:
$$C_\mathcal{M}:=\mathcal{H}^{\dim_{\text{H}}(X_1)}(X_1\setminus X)=0$$ Question: Is there a measure of discontinuity which satisfies the criteria below? (My attempt to answer this question is on Section #3.) If the attempt is correct (i.e., see Sec. 3.3 of File #3 for evidence), it's still extremely long. Is there a easier measure that satisfies all the criteria?
#2. Criteria for the Measure:
Suppose $X\subseteq\mathbb{R}$ and $Y\subseteq\mathbb{R}$ are arbitrary sets, where $f:X\to Y$ is a function. Moreover, $\dim_{\text{H}}(\cdot)$ is the Hausdorff dimension and $\mathcal{H}^{\dim_{\text{H}}(\cdot)}(\cdot)$ is the Hausdorff measure in its dimension on the Borel $\sigma$-algebra. Note, $X_1\subseteq\mathbb{R}$ is an arbitrary set and $X'=X\cap X_1$.
(1) The measure of discontinuity must range between zero and positive infinity
(2) When $X\cap X_1$ is empty, the measure is zero regardless of $\dim_{\text{H}}(X\cap X_1)$ and $\dim_{\text{H}}(X)$
(3) When $f$ is discrete but $X\cap X_1$ is non-empty, the measure is $+\infty$ regardless of $\dim_{\text{H}}(X)$ and $\dim_{\text{H}}(X\cap X_1)$
(4) When the function is continuous on $X_1$, the measure is zero.
(5) When $f$ is "hyper-discontinuous", the measure is positive infinity.
(6) When the closure of the graph of $f$ can be split into a minimum of $n$ function continuous on a positive measure subset of $X_1$ where any vertical line, whose $x$-intercepts are elements of $X$, intersects the limit points $m$ to $n$ times ($m<n$):
(6.1) If $\dim_{\text{H}}(X\cap X_1)<\dim_{\text{H}}(X)$, the measure is a number between $m-1$ and $n-1$ where:
(6.1.1) the variable $\mathfrak{c}$ is the number of the times the vertical line intersects the closure with respect to its $x$-intercept
(6.1.2) $\limsup_{j\to\infty}\mathbf{X}_j'=\liminf_{j\to\infty}\mathbf{X}_j'=X'$ (i.e., the set theoretic limit) such that $0<\mathcal{H}^{\dim_{\text{H}}(X')}(\mathbf{X}_{j}')<+\infty$ for all $j\in\mathbb{N}$
(6.1.3) the arbitrary set ${\overline{X_\mathfrak{c}}}\subseteq X\cap X_1$ has the largest Hausdorff measure in the Hausdorff dimension of $X\cap X_1$, such that the vertical line for all $x\in \overline{X_{\mathfrak{c}}}$ intersects the closure $\mathfrak{c}$ times ($m\le \mathfrak{c}\le n$)
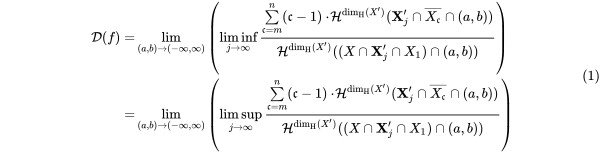 (6.2) If $\dim_{\text{H}}(X\cap X_1)=\dim_{\text{H}}(X)$, and corresponds to the weighted average $\mathcal{D}(f)$
(6.2) If $\dim_{\text{H}}(X\cap X_1)=\dim_{\text{H}}(X)$, and corresponds to the weighted average $\mathcal{D}(f)$(6.3) If $\dim_{\text{H}}(X_1)>\dim_{\text{H}}(X)$, the measure is positive infinity
(7) When the graph of $f$ is dense in the closure of $X'\times Y$, where we remove the subset of the graph of $f$ with zero Hausdorff measure in its dimension and left with the minimum of $n$ functions continuous on a positive measure subset of $X_1$:
(7.1) If $\dim_{\text{H}}(X\cap X_1)<\dim_{\text{H}}(X)$, the measure is zero
(7.2) If $\dim_{\text{H}}(X\cap X_1)=\dim_{\text{H}}(X)$, the measure is $n-1$
(7.3) If $\dim_{\text{H}}(X_1)>\dim_{\text{H}}(X)$, the measure is positive infinity
(8) When the graph of $f$ is dense in the closure of $X'\times Y$, where the graph has zero Hausdorff measure in its dimension, the measure is positive infinity.
#3. Attempt To Define A Measure:
You can ignore this section, though parts of this can be used for a better answer. (I will post a paper with examples showing my measure satisfies the criteria in Section #2.)
Suppose:
• $X\subseteq \mathbb{R}$, $Y\subseteq\mathbb{R}$, and $Y\subseteq\mathbb{R}$ are arbitrary sets
• $f:X\to Y$ is a function
• $d\in[0,1]$
• $\dim_{\text{H}}(\cdot)$ or $d^{\prime}(\cdot)$ is the Hausdorff dimension
• $\mathcal{H}^{\dim_{\text{H}}(\cdot)}(\cdot)$ is the Hausdorff measure in its dimension on the Borel $\sigma$-algebra
• $d_1=\dim_{\text{H}}(X_1)$
• $X'=X\cap X_1$
• $X'\cap(a,b)=X'(a,b)$
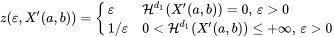 • $\limsup_{j\to\infty}X_{j}(a,b)=\liminf_{j\to\infty}X_j(a,b)=X'(a,b)$ such that $0<\mathcal{H}^{d_1}(X_{j}(a,b))<+\infty$ for all $j\in\mathbb{N}$
• $\limsup_{j\to\infty}X_{j}(a,b)=\liminf_{j\to\infty}X_j(a,b)=X'(a,b)$ such that $0<\mathcal{H}^{d_1}(X_{j}(a,b))<+\infty$ for all $j\in\mathbb{N}$• $\mathbf{R}(X_j(a,b))=\inf\{\mathcal{H}^{\dim_{\text{H}}(\text{Range}(f))}(R): R\subseteq Y, \mathcal{H}^{d_1}(f^{-1}[R]\cap X_j(a,b))=\mathcal{H}^{d_1}(X_j(a,b))\}$
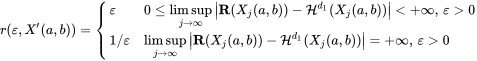 • $G(X'(a,b))$ is the graph of $\left.f\right|_{X'(a,b)}$
• $G(X'(a,b))$ is the graph of $\left.f\right|_{X'(a,b)}$•$\limsup_{j\to\infty}\mathsf{G}_{j}(X(a,b))=\liminf_{j\to\infty}\mathsf{G}_j(X(a,b))=G(X'(a,b))$, where for all $j\in\mathbb{N}$, $0<\mathcal{H}^{d_1}(\mathsf{G}_{j}(X(a,b)))<+\infty$
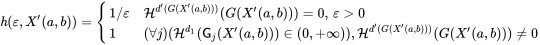 • $\mathcal{P}_{k}(d,G(X'(a,b)))=\left\{\mathbf{G}\subseteq G(X(a,b)):\mathcal{H}^{d_1}(\mathbf{G})=k\right\}$
• $\mathcal{P}_{k}(d,G(X'(a,b)))=\left\{\mathbf{G}\subseteq G(X(a,b)):\mathcal{H}^{d_1}(\mathbf{G})=k\right\}$• $G_k(d,X'(a,b))\in\mathcal{P}_{k}(d,G(X'(a,b)))$
• $\mathbb{G}_{0}(d,X'(a,b))$ is all limit points of $G(X'(a,b))\setminus G_0(d,X'(a,b))$
• $\#|\cdot|$ is the counting measure
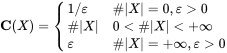 • $\ell(X'(a,b))\subset \mathbb{R}^2$ is an arbitrary, vertical line whose $x$-intercept is an element of $X'(a,b)$
• $\ell(X'(a,b))\subset \mathbb{R}^2$ is an arbitrary, vertical line whose $x$-intercept is an element of $X'(a,b)$• $\mathtt{C}_0(d,\ell,X'(a,b))=\inf\limits_{{G}_{0}(d,X'(a,b))\in\mathcal{P}_{0}(d,X(a,b))}\mathbf{C}(\mathbb{G}_{0}(d,X'(a,b))\cap\ell(X'(a,b)))$
Then, when defining:
• $\limsup_{j\to\infty}\mathbf{X}_{j}(a,b)=\liminf_{j\to\infty}\mathbf{X}_j(a,b)=X'(a,b)$ such that $0<\mathcal{H}^{\dim_{\text{H}}(X')}(\mathbf{X}_{j}(a,b))<+\infty$ for all $j\in\mathbb{N}$
• $\mathbf{M}(\varepsilon,d,\ell,X'(a,b))=z(\varepsilon,X'(a,b))\cdot r(\varepsilon,X'(a,b))\cdot \mathtt{C}_{0}(d,\ell,X'(a,b))\cdot\mathit{h}(\varepsilon,X'(a,b))$
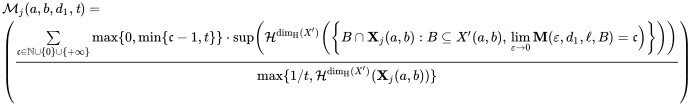 $\mathcal{D}_{d_1}$ is the $d$-dimensional measure of discontinuity (when the limit exists)$$\mathcal{D}_{d_1}=\lim\limits_{(a,b)\to(-\infty,\infty)}\left(\lim_{t\to\infty}\big(\liminf_{j\to\infty}\mathcal{M}_j(a,b,d,t)\big)\right)\\ \quad\;\quad=\lim\limits_{(a,b)\to(-\infty,\infty)}\left(\lim_{t\to\infty}\big(\limsup_{j\to\infty}\mathcal{M}_j(a,b,d,t)\big)\right)$$
$\mathcal{D}_{d_1}$ is the $d$-dimensional measure of discontinuity (when the limit exists)$$\mathcal{D}_{d_1}=\lim\limits_{(a,b)\to(-\infty,\infty)}\left(\lim_{t\to\infty}\big(\liminf_{j\to\infty}\mathcal{M}_j(a,b,d,t)\big)\right)\\ \quad\;\quad=\lim\limits_{(a,b)\to(-\infty,\infty)}\left(\lim_{t\to\infty}\big(\limsup_{j\to\infty}\mathcal{M}_j(a,b,d,t)\big)\right)$$
 Bharathk98
Bharathk98
91
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- unanswered
- 1500 views
- $100.00
Related Questions
- Calculate the following, if it exists: $\int_{0}^{1} x^a(lnx)^mdx$ , where $a > -1$ and $m$ is a nonnegative integer.
- Calculate $\iint_R (x+y)^2 e^{x-y}dx dy$ on the given region
- Use Rouche’s Theorem to show that all roots of $z ^6 + (1 + i)z + 1 = 0$ lines inside the annulus $ \frac{1}{2} \leq |z| \leq \frac{5}{4}$
- A problem on almost singular measures in real analysis
- Prove that every compact Hausdorff space is normal
- Finding a unique structure of the domain of a function that gives a unique intuitive average?
- What is the asymptotic density of $A$ and $B$ which partition the reals into subsets of positive measure?
- Calculus - stationary points, Taylor's series, double integrals..

I made some corrections.
Please respond.
I added a file with evidence that my measure of discontinuity is correct.
It seems it's difficult to find a taker for the question. I would suggest to try to make it simpler and easier to understand. E..g, in the 1st phrase you say "X, X1 and Y are sets *such that* f:X-Y is a function". That doesn't make sense. You should say "f : X -> Y is a function from X \subset ... to Y \subset..." There is no X1 so far. In the 2nd phrase you say "f is ...disconnected on X' x Y", but X' was never defined. Etc...
@MFH Thank you for responding. The beggening should be clear now.