Calculus: INFINITE SERIES
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
3 Attachments
Kav10
1.9K
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 414 views
- $40.00
Related Questions
- Custom Solutions to Stewart Calculus, Integral
- highschool class help
- using maclaurin series for tan(x) and equation for length of cable to prove that x=
- Use the equation to show the maximum, minimum, and minimum in the future.
- Characterizing the Tangent and Normal Bundles - Submanifolds in Banach Spaces and Their Classifications
-
Limit graphs
- Find the amount of work needed to pump water out of full spherical tank
- Answer is done,
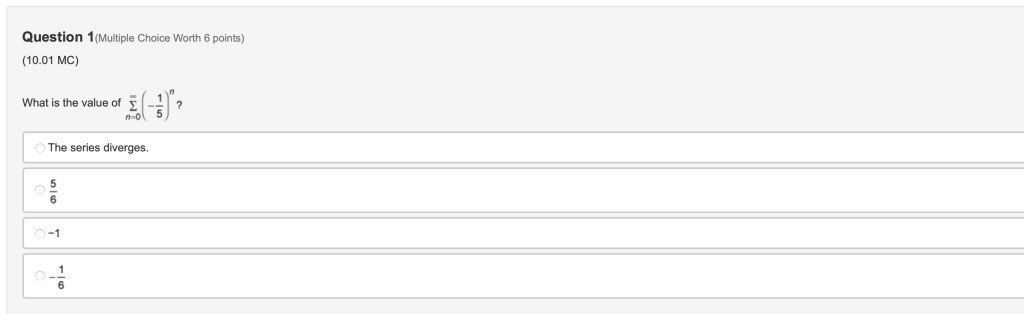
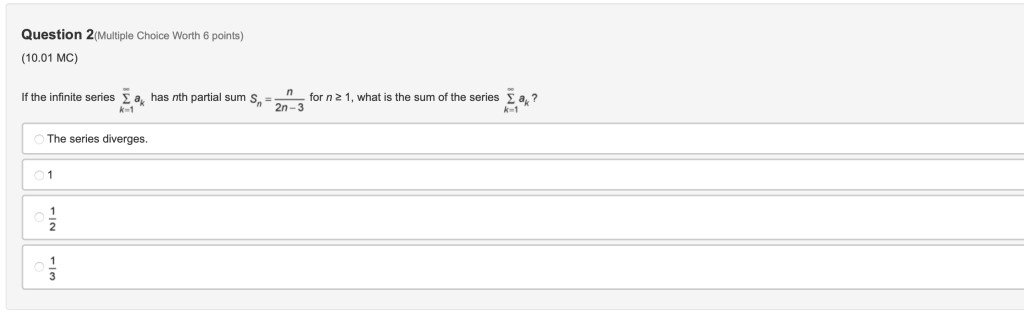
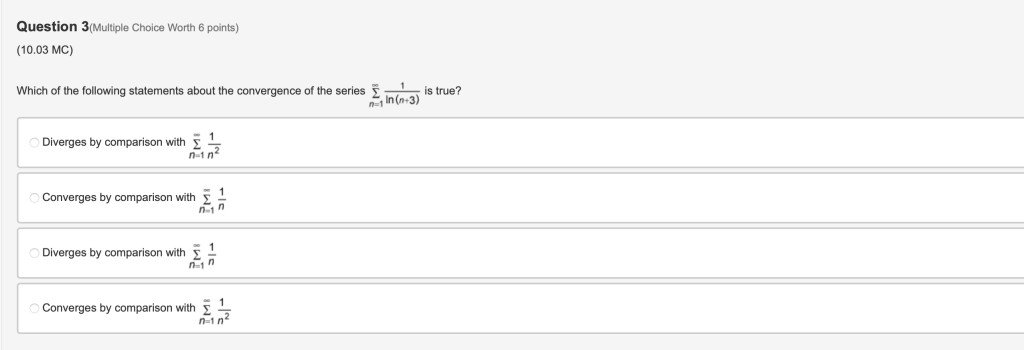
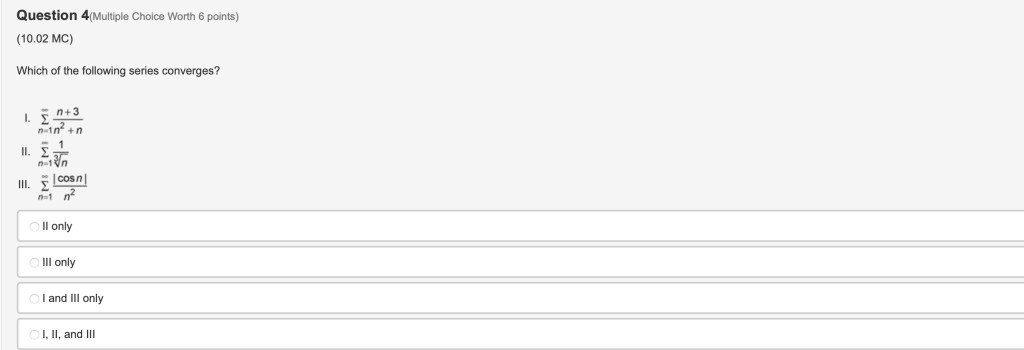
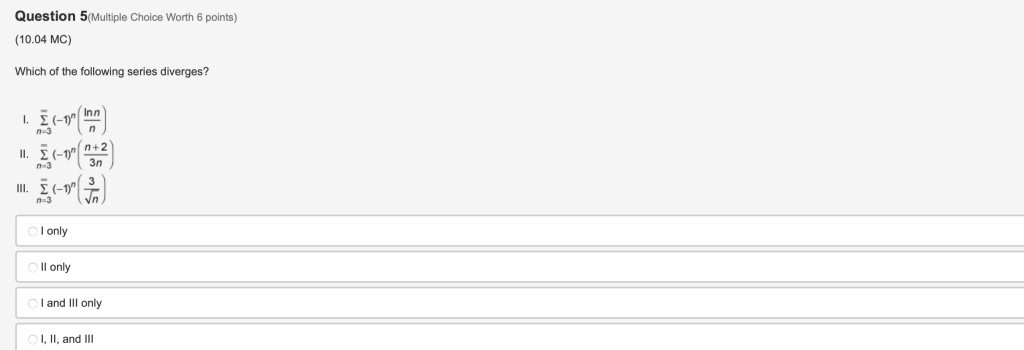
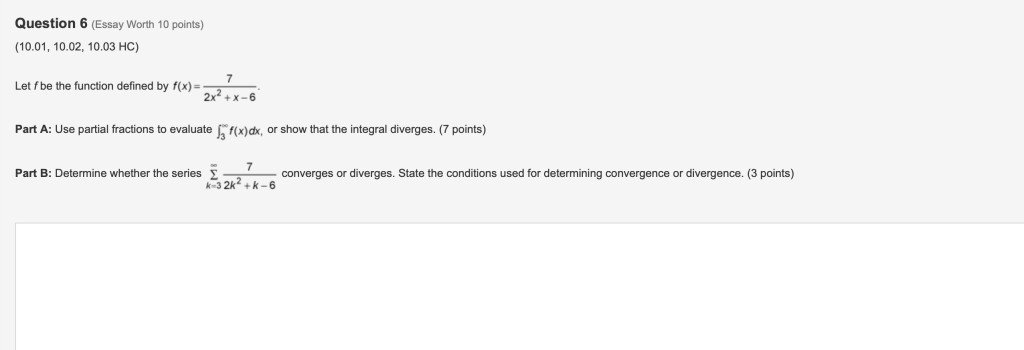
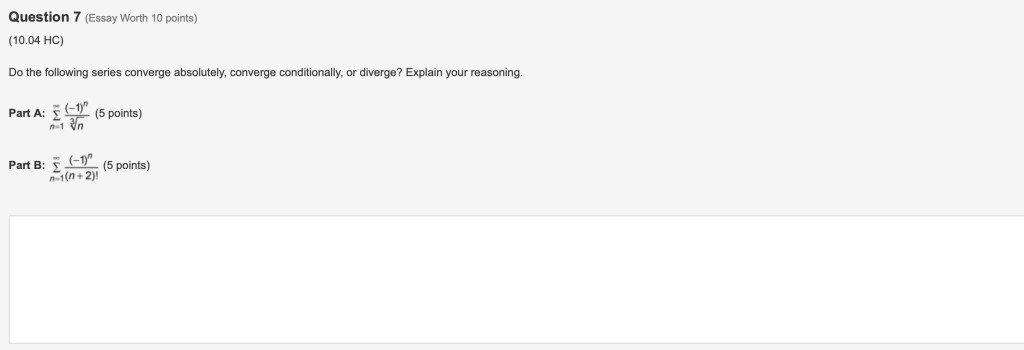
You can answer whenever you want; I will have three projects Tomorrow (Sunday) if you wanna answers (high bounty).
Yes, got it. Thanks.
YOU'RE AWESOME
Sure. What time tomorrow?
around 2 o'clock
Pacific or Eastern?
EDT, so eastern
Sounds good. I am in the west, so 11 am my time.
For the MCQ Above, give me the answer option to check if mine matches. And for the written, just be organized as always! THANKS
Sure. NO PROBLEM.