[Help Application of Integration]Question

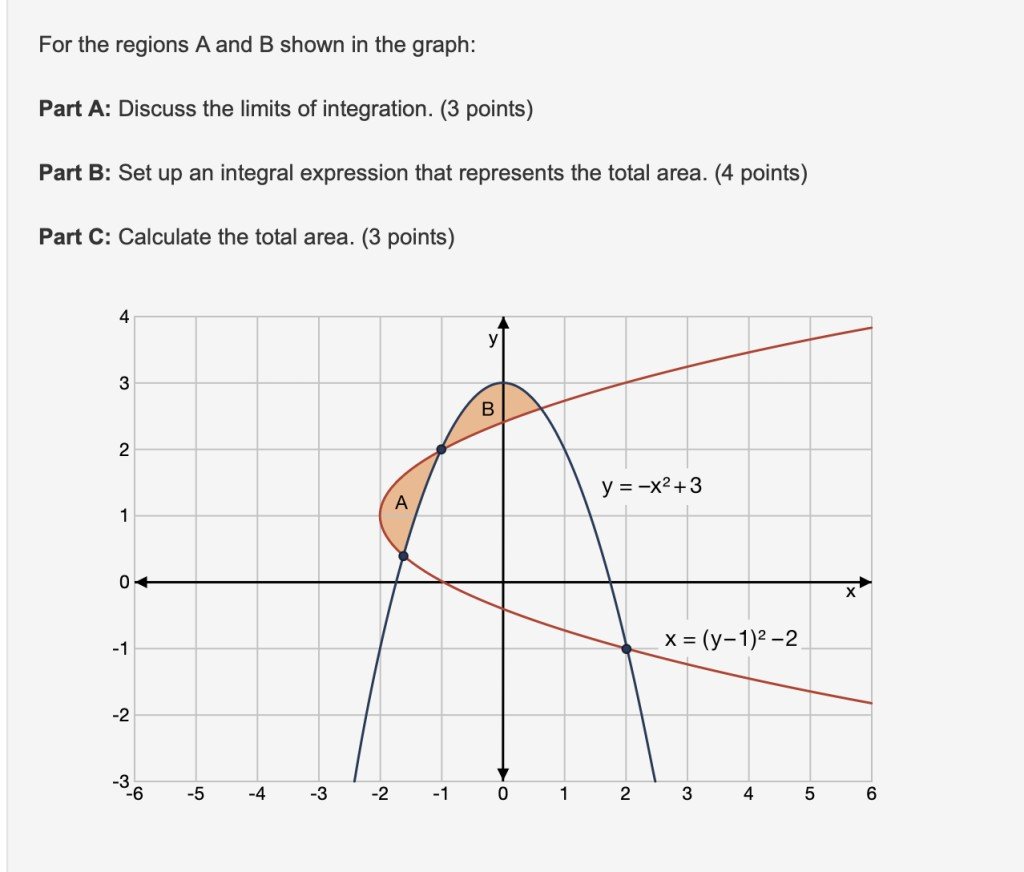
Part A:

The curves $y = -x^2 + 3$ and $x = (y-1)^2 - 2$ intersect in 4 locations as can be seen on the diagram. The limits of integration for $A$ are the second and third highest $y$-coordinates of this intersection. There will be two intersections, representing the lower and upper limits respectively. Let us solve  for the intersection. Plugging the second equation into the first, we obtain $y = -((y-1)^2 - 2)^2 + 3 = -(y^2 - 2y - 1)^2 + 3 = -y^4 +4y^3 -  2y^2 - 4y +2$.

Thus the equation simplifies to

$$y^4 - 4y^3 + 2y^2 + 5y - 2 = 0.$$

By inspection, we see that $-1$ and $2$ are solutions to this equation. Using polynomial division, we obtain

$$(y-2)(y+1)(y^2 - 3y + 1) = 0.$$

Applying the quadratic formula to the quadratic expression, we obtain that the roots to the quadratic are $\frac{1}{2}(3 - \sqrt 5)$ and $\frac{1}{2}(3 + \sqrt 5)$. Thus the complete list of roots in ascending order are

$$-1, \frac{1}{2}(3 - \sqrt 5), 2, \frac{1}{2}(3 + \sqrt 5).$$

It follows that the limits of integration for $A$ are $y = \frac{1}{2}(3 - \sqrt 5)$ and $y = 2$.

The limits for $B$ on the other hand will be the $x$-coordinates of the intersections with the two highest $y$ coordinates. Thus plugging in $y = 2$  and $y = \frac{1}{2}(3 + \sqrt 5)$ into the expression $ x = (y-1)^2 -2$, we obtain that the limits are $x = -1$ and $x = \frac{1}{2}(\sqrt 5 - 1)$.

Part B:


To obtain an integral expression for $A$, we first invert the curve $y = -x^2 + 3$ and take the lower branch. This has inverse $x = -\sqrt {3-y}$. Thus an integral expression for $A$ is given by integrating the difference of the two curves:

$$A = \int_{ \frac{1}{2}(3 - \sqrt 5)}^2 - \sqrt {3-y} - (y-1)^2 + 2 \, dy.$$

Similarly, inverting $x = (y-1)^2 - 2$ and taking the upper branch gives us $y = 1 + \sqrt{x + 2}$. Thus

$$B = \int_{-1}^{\frac{1}{2}(\sqrt 5 - 1)}  -x^2 +2  - \sqrt{x+2},$$

and an expression for the total area $A + B$ is given by

$$ \int_{ \frac{1}{2}(3 - \sqrt 5)}^2 - \sqrt {3-y} - (y-1)^2 + 2 \ \, dy+ \int_{-1}^{\frac{1}{2}(\sqrt 5 - 1)}  -x^2 +2 - \sqrt{x+2} \, dx.$$

Part C:

To calculate the total area, we just need to evaluate the integral expression in part $B$ for the total area. We compute

$$\text{Total Area} = \int_{ \frac{1}{2}(3 - \sqrt 5)}^2 - \sqrt {3-y} - (y-1)^2 + 2 \, dy+ \int_{-1}^{\frac{1}{2}(\sqrt 5 - 1)}  -x^2 +2 - \sqrt{x+2} \, dx.$$
 $$ = [ \frac{2}{3} (3-y)^{3/2} - \frac{1}{3}(y - 1)^3 + 2y ]_{ \frac{1}{2}(3 - \sqrt 5)}^2 + [-\frac{1}{3}x^3 + 2x - \frac{2}{3}(x+2)^{3/2}]_{-1}^{\frac{1}{2}(\sqrt 5 - 1)}.$$
$$ = \frac{2}{3} + \frac{2}{3}$$
$$= \frac{4}{3}.$$