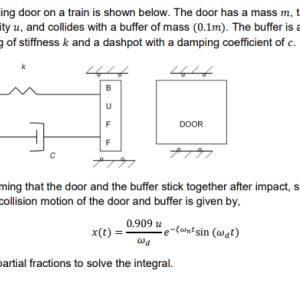
Equations of Motion and Partial Fractions
The question is asking you to find the equation of the displacement for the object (door+buffer) after the collision. You can find the displacement equation x(t) by first finding the equation of motion of the system post-collision, which is a 2nd order ODE (function of d(dx/dt)/dt), and then integrating. The question is asking you to use the method of partial fractions to solve that integral.
Use a freebody diagram to aid this solution.
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
1 Attachment
Kav10
-
A few questions regarding this solution. 1) On sheet 2 you say 'we have 𝑀 = 𝑚 + 0.1𝑚 = 1.1𝑚 (𝑘𝑔)' - Where does this come from? 2) you then introduce 𝜔n & 𝜉, where do these come from / what are they? 3) on page 3 you introduce A and B, what do these represent? 4) page 4 you say 'we have 𝑆in(𝜔𝑑𝑡) =(𝑒^𝑖𝜔𝑑𝑡 − 𝑒^-𝑖𝜔𝑑𝑡) /2𝑖' where do we have this from? Im not sure i follow. Lastly 5) the question asks to solve this eqution using partial fractions?
-
1) See the question, door has mass m, buff has mass 0.1m. This is total mass! 2) These are the same variables as introduced in the question. See the formula. These are given assumptions. 3) See a couple of lines before introducing A, comes from standard solution of the differential equation introduced before. 4) Similar to 2 and 4, also a given. 5) Yes, partial fraction is used. Google partial fractions and read more about it. Thanks.
-
-
Ok thanks for your quick response. Im still not entirley sure where the variables in 2) come from. what do 𝜔n & 𝜉 stand for / mean?
-
Please go ahead and the chapter related to these concepts related to angular speed and motion. You can start with this: https://en.m.wikipedia.org/wiki/Angular_momentum
-
-
Thanks i will read through this, i guess im just a bit confused as to how this system has angular momentum when the door is sliding horizontally?
-
That is any speed snd motion not just angular.
-
-
Having read through this im still not really following what 𝜉 is and what wn are. with regards to the equation where we introduce 𝜉 why is there 2.2 on the bottom of fraction?
-
Do you know what 𝜉 is in the question? 2.2 is an assumption to get to get to the 2wn in the line after it .
-
-
If you read all those I sent and still confused about the solution, I am not sure how else I can help you understand the concepts and formulas related to this question. Sorry.
-
You need to read a lot basics in order to understand natural frequency, damped frequency, and dynamics and vibration in general. This is an advanced question which needs those background. I don’t think I can help you more given the time and bounty.
-
-
Ok i think for the most part i now follow this. 1 question i have though is at the stage where we let 𝑥 = 𝐴e^mt. Is 𝑥 = 𝐴e^mt a standard formula? As i cant see where we would derive this from? If it is standard formula what actually is it?
-
That is a standard solution of a differential equation in the form of shown in the solution I provided (e.g. aX"+bX'+cX=0).
-
-
Unlikely Plum, remember you said you’ll pay at least $30 for this complex question. I don’t think you’ve done that yet.
-
Wow! Good job “deleted_account_60”, for only 10 dollars? Haha
- answered
- 951 views
- $20.00
Related Questions
- Help with Norms
- A bicycle with 18in diameter wheels has its gears set so that the chain has a 6 in. Radius on the front sprocket and 4 in radius on the rear sprocket. The cyclist pedals at 180 rpm.
- Find the average value of the function $\frac{\sin x}{1+\cos^2 x}$ on the interval $[0,1]$
- Evaluate $\int_0^{\frac{\pi}{2}}\frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}} dx$
- Vector-Valued Equations
- You have a piece of 8-inch-wide metal which you are going to make into a gutter by bending up 3 inches on each side
- Differentiate $f(x)=\int_{\sqrt{x}}^{\sin^2 x}\arctan (1+e^{t^2})dt$
- Beginner Question on Integral Calculus
This needs a lot more work. Bounty is low.
I second that!
i could add a $10 tip for correct answer and working?
The answer to this question would be at least a couple of pages. I think a fair bounty is $50.
ah sorry about that, however it is outwith my budget :(
That's OK. $30 is the max you can pay?
yeah id say so. i guess max could be 35
OK, I'll do it for you this time :-)
many Thanks