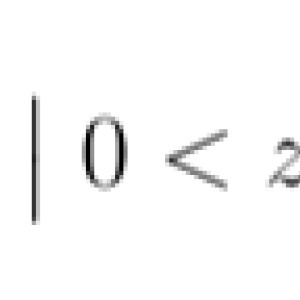Calculus 2 / Calculate the surface of F
My problem is exactly what it says in the title. I need to calculate the surface of F, and honestly I have no idea how. Help would be much apreciated.
Answer
$F$ is the surface of revolution of the curve $x = z^3$ rotated along the $z$-axis. Using the formula for such surfaces (see for example https://en.wikipedia.org/wiki/Surface_of_revolution), we have that
\[ S(F) = 2\pi \int_0^1 z^3 \sqrt{1 + \left(\frac{dx}{dz}\right)^2} dz = 2\pi \int_0^1 z^3 \sqrt{1 + (3z^2)^2} dz = 2\pi \int_0^1 z^3 \sqrt{1 + 9z^4} dz. \]
The indefinite integral for $z>0$ is not difficult to calculate: up to a constant it is of the form \[ \int f'(z)\sqrt{(f(z))}dz. \] Let $f(z) = 1 + 9z^4$. We have
\[ 2\pi \int_0^1 z^3 \sqrt{1 + 9z^4} dz = \frac{2\pi}{36} \int_0^1 f'(z) \sqrt{(f(z))} dz = \frac{2\pi}{36} \frac{2}{3} f(z)^{3/2} \rvert_0^1 = \frac{\pi}{27} \left. (1 + 9 z^4)^{3/2} \right\rvert_0^1, \]
so \[ S(F) = \frac{\pi}{27}(10\sqrt{10}-1). \]
Alessandro Iraci
- answered
- 921 views
- $12.70
Related Questions
- Profit maximizing with cost and price functions
- Two calculus questions
- Find $\lim\limits _{n\rightarrow \infty} n^2 \prod\limits_{k=1}^{n} (\frac{1}{k^2}+\frac{1}{n^2})^{\frac{1}{n}}$
- Evaluate $\int \ln(\sqrt{x+1}+\sqrt{x}) dx$
- Show that the distance between two nonparallel lines is given by $\frac{|(p_2-p_1)\cdot (a_1\times a_2)|}{|| a_2\times a_1||}$
- Generalization of the Banach fixed point theorem
- Calculate the superficial area
- Method of cylindrical shells
