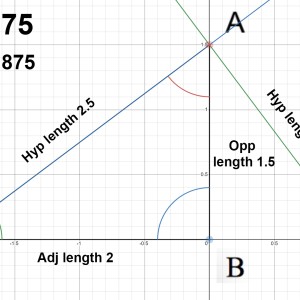
Why if $\frac{opp}{adj} =x$, then $x \times hyp =$ The length of a line perpendicular to the hypotenuse with the same height.
Why if $\frac{opp}{adj} =x$, then
$x \times hyp =$ The length of a line perpendicular to the hypotenuse with the same height.
So if you have a triangle and you divide the opposite by the adjacent, the ratio you get can be used to multiply the hypotenuse to get the length of a line perpendicular to the hypotenuse with the same height.
What exactly is happening why does this work?
See the file attached for a more visual representation.
Math Gnome
87
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
Erdos
4.7K
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1606 views
- $5.00
Related Questions
- How to recalculate 2D polygon side lengths when tilt is applied in 3D space?
- How do I negate the effect that the rotation of a plane has on a rectangle?
- Probability that the distance between two points on the sides of a square is larger than the length of the sides
- Determine the surface area of a ball, rotating a function about $x$-axis.
- Help finding the internal angles of my bike frame
- Can enough pizza dough be made to cover the surface of the earth?
- Calculating aspect ratio limits of rotated rectangle within a rectangle
- Petra is organising a team building activity day with work colleagues . She is considering two options, which both offer packages for groups of up...
