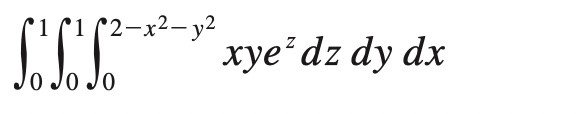Custom Solutions to Stewart Calculus, Integral
Answer
Sure, you came to the right place to get custom solutions given by experts.
For this integral we start by integrating with respect to $z$ : $$ \int _0 ^1 \int _0 ^1 \int_0 ^{2-x^2-y^2} xy e^{z}\,dz\,dy\,dx = \int _0 ^1 \int _0 ^1 xy e^{z}\,\Big]_0 ^{2-x^2-y^2}\,dy\,dx \\ = \int _0 ^1 \int _0 ^1 xy( e^{2-x^2-y^2}-1)\,dy\,dx. $$
Then we do the $y$ integral. For this let $u=2-x^2-y^2$ to get $du=-2ydy$ (remember that in the $y$ integral we treat $x$ as a constant!)
$$ \int _0 ^1 \int _0 ^1 xy( e^{2-x^2-y^2}-1)\,dy\,dx \\ \; \\ =\int _0 ^1 \int _0 ^1 \frac{-1}{2}x (e^{u}-1)\,du\,dx = \int _0 ^1 \frac{-1}{2}x (e^{u}-u)\,\Big]_0 ^1\,du\,dx \\ \; \\ =\int _0 ^1 \frac{-1}{2}x (e-2)\,dx = \frac{-(e-2)}{2}\,\frac{x^2}{2}\,\Big]_0 ^1 = \frac{-(e-2)}{4}$$
- accepted
- 580 views
- $15.00
Related Questions
- Find the average value of the function $\frac{\sin x}{1+\cos^2 x}$ on the interval $[0,1]$
- Convergence of $\int_{1}^{\infty} e^{\sin(x)}\cdot\frac{\sin(x)}{x^2} $
- Show that the distance between two nonparallel lines is given by $\frac{|(p_2-p_1)\cdot (a_1\times a_2)|}{|| a_2\times a_1||}$
- What is the integral of (x^2-8)/(x+3)dx
- Help with Business calculus. Finding derivative for X of given function.
- Differentiate $f(x)=\int_{\sqrt{x}}^{\arcsin x} \ln\theta d \theta$
- Vector field
- Need help with integrals (Urgent!)
