Compound Interest with monthly added capital
The thing is: I really don't like not being able to use only one formula to deduct a monthly compound interest with and addition of ×$ every month.
Usually, I would be solving it by using the interest formula and adding x amount for every month, as demonstrated:
10.000$ of Principle 10% of rate (time in months)
In the 1st month i would have 11.000$ with the addition of 1000, that i chose to add every month, so 12.000 to begin the 2nd month with
12.000$ Principle 10% of rate +1.000$ extra one more time 13.200 + 1.000; i would have 14.200$ for the 3rd month.
That's too much job.
Me and a colleague of mine developed 2 different formulas that seem to work, but not every time
The first one works pretty well with the example I first gave: 10.000$, 10% interest /month and +1000$ every month for 3 months.
The second one seems to work with 20.000$, 10% interest/month and +500$ every month for 4 months.
Any ideas?
(Captions: M=Accumulated amount; C=Principle;
i-interest; x=added value
for a 10% monthly interest I used i = 0,1)
Answer
Let $M_n$ be the accumulated amount after $n$ accumulations. Then we have
\[M_n=M_{n-1}i+M_{n-1}+x=M_{n-1}(1+i)+x.\]
Thid means that the accumulated amount after $n$ months is equal to the accumulated amount in the previous month plus the interest earned during the month plus the added value $x$.
Hence
\[M_n=M_{n-1}(1+i)+x=[M_{n-2}(1+i)+x](1+i)+x\]\[=M_{n-2}(1+i)^2+x(1+i)+x.\]
So
\[M_n=M_{n-2}(1+i)^2+x(1+i)+x.\]
Repeating this process we get
\[M_n=M_{0}(1+i)^n+x(1+i)^{n-1}+\dotsx +x(1+i)+x.\]
So
\[M_n=M_{0}(1+i)^n+x[(1+i)^{n-1}+\dotsx(1+i)+1]\]\[=M_0(1+i)^n+x[\frac{(1+i)^{n}-1}{i+1-1}]\]
\[=M_0(1+i)^n+\frac{x}{i}((1+i)^{n}-1).\]
Since $M_0=C$, we get the fomula
\[M_n=C(1+i)^n+\frac{x}{i}\big((1+i)^{n}-1\big).\]
For monthly accumulations with yearly interest rate $I$ we have $i=\frac{I}{12}$. For $I=10\%=\frac{10}{100}$, you should set
\[i=\frac{I}{12}=\frac{\frac{10}{100}}{12}=\frac{1}{120}.\]
Erdos
-
love this one! one thing tho: using it to solve 10.000$ 10% +1000/month for 3 months gives me 16620$, when it should be 15620$ but using 20.000$ 10% +500/month for 4 months equals to 31.602,5$, which is correct what do you think is causing this?
-
For 10.000$, 10% +1000/month for 3 months I am getting $13277.15. For 10.000$, 10% +1000/month for 4 months I am getting $14387.80. Your numbers seems incorrect. Please double check your work. 15620 for 3 months is incorrect. After three months you have deposited 10,000+3000. 15620-13000=2620 is too much of an interest for only three month!
-
maybe i misunderstood your formula because of the language barrier, for 10.000$, 10% + 1000/month for 3 months this is the way i understood it: Mn= 10.000(1+0,1)^3 +1000/0,1 x ((1+0,1)^4 -1) what am i missing? sorry to bother
-
You probably did not pay attention to the last paragraph. In this case i=1/120 and not 0.1. You will get: M_3=10.000(1+1/120)^3 +1000/(1/120) x ((1+1/120)^3 -1)=14387.80. There is no language barrier here, you just need to read my solution more carefully.
-
- answered
- 936 views
- $2.00
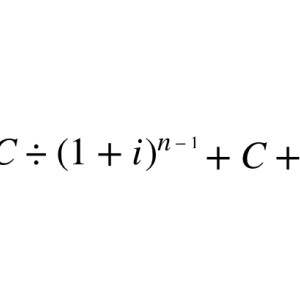
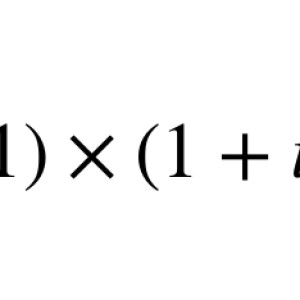
The offered bounty is low for the level of the question and the amount of time one needs to carefully answer this question.
i am so sorry, it was not my intention! i live in a 3rd world country and i cannot pay more than this :(