Poker Outcomes and Variance: Calculating Likelihood of an Observed Outcome
I would like to learn how to calculate and interpret the likelihood of the following example poker scenario:
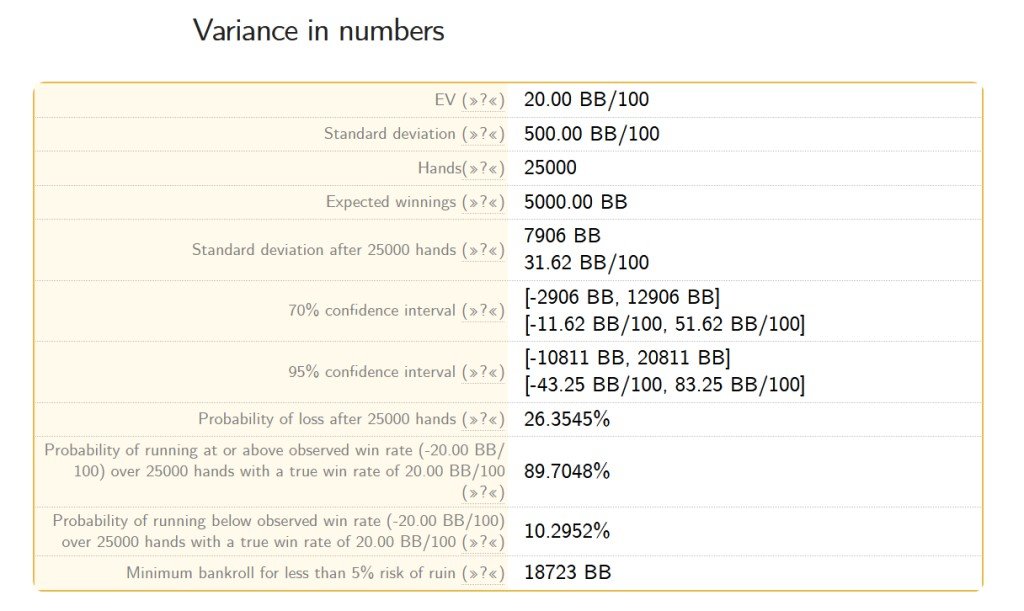
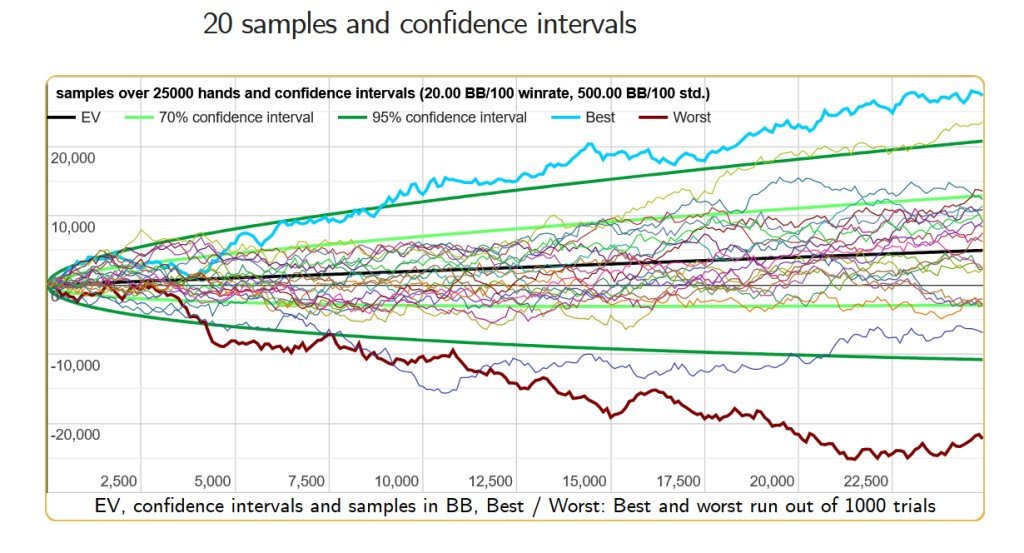
Sample (number of hands): 25,000
Winrate in BB/100 Expected Value: +20 BB/100
Winrate in BB/100 Observed: -20 BB/100
Standard Deviation BB/100: 500 BB/100
For those unfamiliar with BB/100 notation, the BB value represents the stake level (e.g. BB = 2 dollars), and the /100 means per 100 hands. In this example, +20 BB/100 = 40 dollars per 100 hands = 0.40 dollars (40 cents) per hand in expected winnings.
1. Can we precisely calculate the probability that this result is observed given these inputs? i.e. exactly how likely is this 40 BB/100 difference between our EV and what actually happened?
2. Is there a general formula which can be used to calculate such a liklihood given any set of input variables (e.g. smaller/large samples, different winrates/std dev, etc)?
I have plugged these values into a poker variance calculator and got the following results, but I do not understand how to interpret them correctly:
 Justq
Justq
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
 Martin
Martin
- answered
- 1799 views
- $20.00
Related Questions
- Slot Machine Probability
- Summation of Catalan Convolution
- Maximum Likelihood Estimation
- Probability
- Probability that a pump will fail during its design life
- Using probability to calculate expected time a task would take with "bad" luck
- Operational Research probabilistic models
- Combinatorics questions- can someone please help?