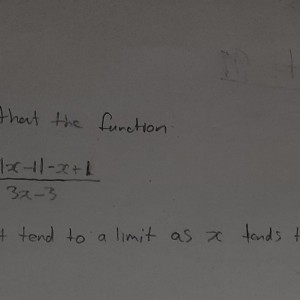Prove the Function
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
 Dynkin
Dynkin
779
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1483 views
- $5.00
Related Questions
- Uniform convergence of functions
- A function satifying $|f(x)-f(y)|\leq |x-y|^2$ must be constanct.
- How to derive the term acting like a first derivative with respect to A that I found by accident?
- Prove that $f$ is a diffeomorphism $C^∞$, that maps... (More inside)
- Let $f\in C (\mathbb{R})$ and $f_n=\frac{1}{n}\sum\limits_{k=0}^{n-1} f(x+\frac{k}{n})$. Prove that $f_n$ converges uniformly on every finite interval.
- Let $(X, ||\cdot||)$ be a normed space. Let $\{x_n\}$ and $\{y_n\}$ be two Cauchy sequences in X. Show that the seqience Show that the sequence $λ_n = ||x_n − y_n|| $ converges.
- Banach fixed-point theorem and the map $Tf(x)=\int_0^x f(s)ds $ on $C[0,1]$
- Prove that if $T \in L(V,W)$ then $ \|T\| = \inf \{M \in \R : \, \|Tv\| \le M\|v\| \textrm{ for all } v \in V \}.$