ODE pls help solve
Find a factor Q(t,y) that makes this equation exact, please include some steps
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
 Dynkin
Dynkin
779
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1203 views
- $3.00
Related Questions
- Solve the two-way wave equation in terms of $u_0$
- 3 Multi-step response questions
- Dynamic Systems of Differential Equations
- Lyapuniv-functions
- ODEs: Lipschitz-continuity and an IVP
- General solutions of the system $X'=\begin{pmatrix} a & b \\ c & d \end{pmatrix} $
- Solve $Lx = b$ for $x$ when $b = (1, 1, 2)^T$.
- Please solve this question
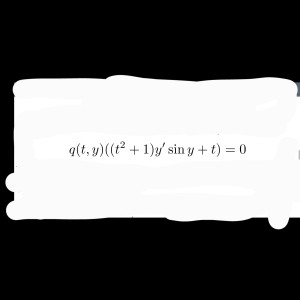

Low bounty!