$Calculating aspect ratio limits of rotated rectangle within a rectangle$

Question

$Calculating aspect ratio limits of rotated rectangle within a rectangle$

Hello !

I was wondering if there would be an equation for this sort of a problem or if the solution might need to be brute forced by approximation.

example image: https://imgur.com/ql9tAxE

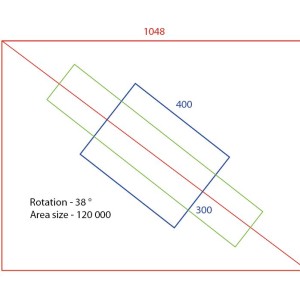
There is a rectangle A (red) of a known size in a 4:3 aspect ratio.Centered inside of A there is another rectangle B (blue) also of 4:3 aspect ratio, which is of variable size and variable rotation.

In my example IMG B is 400x300 and rotated by 38 degrees. I would like to know the formula how to calculate new "wider" aspect ratio of B so that it would retain the area size and touch the "boundaries" set by A. The width of B should be getting bigger while height of B should be decreasing. The whole rectangle should remain in the starting rotation.

I know how to calculate the distance from the corner of B to A, if following the line of B. However whenever I change the ratio the distance changes. And that left me a bit bewildered on how to go about what is the relationship between the ratio and the distance.

I am also aware that if rectangle B's rotation is more than rotation of the A's diagonal it will always touch the top. However, if it is less I am not sure how to determine when it would touch the top or left side of A.

Therefore, I would like to know how to determine that and then how to calculate the new aspect ratio, since the side where the "collision" happens probably affects the way the ratio is calculated.

Thank you very much for any ideas!

Alex

Trigonometry Geometry

Superpowacow

7

Matchmaticians Calculating aspect ratio limits of rotated rectangle within a rectangle File #1

File #1 (jpg)

Report

Daniel90

0

The bounty is low.
M F H

0

Some things are slightly unclear : Do you want a general solution for A = w x h with arbitrary width w & height h ? Also, the 38° rotation, do you want that angle be one of the arbitrarily given parameters, or fixed from the fact that it is (here) the angle between the diagonal and the longer side of A ?
- M F H
  
  0
  
  Given the quite low bounty, I will assume the simplest option and give a formula for the data as given. Then we can generalize later.
- Superpowacow
  
  0
  
  Hello , thank you for the question I will update my post! Yes, the width and height are arbitrary, although the width should be getting bigger and the height smaller. When it comes to the angle... I think if I understand correctly...then I think of it as fixed. (The diagonal line of A should be passing through the middle of the smaller sides of B)
Superpowacow

0

Oh apologies.... about the rotation..... I confused myself. The orientation of rectangle B should basically remain in the starting randomly picked rotation (0-90) in this it case being 38 degrees.
- Superpowacow
  
  0
  
  Oh yes, I am sorry again I was in a rush when replying. Now I understood !!! This seems right "or fixed from the fact that it is (here) the angle between the diagonal and the longer side of A " .... The longer side of A being 0 degrees and the longer side of B being 38 degrees and this should remain so.

Answer

The answer is accepted.

Join Matchmaticians Affiliate Marketing Program to earn up to a 50% commission on every question that your affiliated users ask or answer.

M F H

0

Some things are slightly unclear : Do you want a general solution for A = w x h with arbitrary width w & height h ? Also, the 38° rotation, do you want that angle be one of the arbitrarily given parameters, or fixed from the fact that it is (here) the angle between the diagonal and the longer side of A ?

M F H

0

Given the quite low bounty, I will assume the simplest option and give a formula for the data as given. Then we can generalize later.

Superpowacow

0

Hello , thank you for the question I will update my post! Yes, the width and height are arbitrary, although the width should be getting bigger and the height smaller. When it comes to the angle... I think if I understand correctly...then I think of it as fixed. (The diagonal line of A should be passing through the middle of the smaller sides of B)
M F H

0

Given the quite low bounty, I will assume the simplest option and give a formula for the data as given. Then we can generalize later.
Superpowacow

0

Hello , thank you for the question I will update my post! Yes, the width and height are arbitrary, although the width should be getting bigger and the height smaller. When it comes to the angle... I think if I understand correctly...then I think of it as fixed. (The diagonal line of A should be passing through the middle of the smaller sides of B)
Superpowacow

0

Oh apologies.... about the rotation..... I confused myself. The orientation of rectangle B should basically remain in the starting randomly picked rotation (0-90) in this it case being 38 degrees.

Superpowacow

0

Oh yes, I am sorry again I was in a rush when replying. Now I understood !!! This seems right "or fixed from the fact that it is (here) the angle between the diagonal and the longer side of A " .... The longer side of A being 0 degrees and the longer side of B being 38 degrees and this should remain so.
Superpowacow

0

Oh yes, I am sorry again I was in a rush when replying. Now I understood !!! This seems right "or fixed from the fact that it is (here) the angle between the diagonal and the longer side of A " .... The longer side of A being 0 degrees and the longer side of B being 38 degrees and this should remain so.

Answer 1

Answers can only be viewed under the following conditions:

The questioner was satisfied with and accepted the answer, or
The answer was evaluated as being 100% correct by the judge.

View the answer

Let us simply write the formula for the area of B as function of its height h when its corner touches the border of A. This will (for the given configuration) happen on the upper border near the left and on the lower border near the right. To find the width of the area B, we will focus on the small rectangular triangle on top left, which has its shorter leg of length h/2 and its longer leg of length d = distance of B from the top left corner of A :

[see picture at this URL]

We then have:

w + 2d = $\sqrt{ W² + H² }$ =: D = length of the diagonal of A

i.e.: w = D - 2d, but also :

(h/2) / d = tan $\alpha$ = H / W, so : d = (h/2) * (W/H)

whence: w = D - h * W/H .

The area of B is

area(B) = h * w = h * ( D - h * W/H )

For a given area of B this is a quadratic function of h we can solve for h :

h² - D (H/W) h + area(B) * H/W = 0

h = ½ [ $ D \, H/W \pm \sqrt{ (D \, H/W)² - 4\,{\rm area}(B) \, H/W }$ ]

= ½ D H/W * [ $ 1 \pm \sqrt{ 1 - 4\,W/H\cdot {\rm area}(B) /D² }$ ]

For the given values, H/W = 3/4 ; area(B) = 120 000 ; D = sqrt( 1024² + 768² ) = 1280

we have D H/W = 960 and

h = ½ [ 960 ± sqrt( 960² - 360 000 ) ] = 480 ± 60 $\sqrt{39}$ .

The larger height, with " + ", corresponds to the rectangle where the leftmost and rightmost corner of B would touch the border of A, but then the upper and bottom corners are outside of A. (Not sure if I understand well in your question whether you might be interested in this.)
In the present situation, we have to choose the smaller value, i.e., the " - " sign:

h = 480 - 60 $\sqrt{39}$ = 105.3 ,

and then w = 120 000 / h , or (equivalently)

w = D - h W/H = 1280 - 4/3 * 105.3 = 1139.6. (Double-check: this also gives h * w = 120 000.)

For the aspect ratio, this gives w/h = area(B) / h² = D/h - W/H,
in the present case this is w/h = 10.822
but "h" has to be calculated anyway, using the given formula.

This will work for any aspect ratio. As long as you are in "Landscape" format, it will always be the uppermost and lowermost(?) corners of B that touch the border of A first.

When you switch to "Portrait" mode, it would be the left- and rightmost corners of B, but that will simply exchange the roles of W and H everywhere. So, without loss of generality, you can always choose W > H and the formulas for h (and from there w = area(B)/h) as given above.

I hope this anwers satisfyingly, else please let me know in comments.

M F H

313

M F H

0

argh ! for some reason it does not display correctly the &cdot; (centred dot) and × (cross) for multiplication. You can see them if you look at "View Raw" or at the page given in the "picture" link. But I can replace them by " * " if you wish.
Superpowacow

0

Hello thank you!!! I now tried it out. And it fits exactly for the rotation of A's diagonal line that has the rotation of (36,235). But I wanted the rectangle B to remain in the randomly picked rotation (0-90°) in my example case (38°). https://imgur.com/HTfLoSD I think I might have misled you with my first reply where I confused myself and wrote exactly that..... I can accept the answer, since it is my fault. Would it be possible to tweak it and incorporate the specific angles?
- Superpowacow
  
  0
  
  Would it be possible to tweak it and incorporate various starting rotations 0-90° of B ? I could add a tip or post another question.
M F H

0

Yes that's possible. You can actually use the same formulas with just a different width W = H • tan alpha, because the width is not really relevant (as long as alpha ≤ 45º ; for alpha ≥ 45º, W and H exchange their roles as already mentioned in the answer. If you want I can spell it out in more detail, a tip would be appreciated.
Superpowacow

0

Awesome, thank you !!! Do you mean changing the W like so: https://imgur.com/3NH6mTK ? (instead of 1024 --> 600.02 in this case) Because this way I get even smaller for h and bigger for w. Apologies for being ignorant...
M F H

0

maybe yes, but you still write "rotation 38° " , I guess it is more now, and of course the width (and height) of the blue rectangle should change (as to touch the border with the corner). How to proceed : choose the angle alpha [say 45°]. Compute W = H*tan(alpha) [regardless of the W you had before, e.g. "old" W=1024, just ignore] . [Would give W=H for 45° ; if H=768 then now also W=768 for use in the formulas.] This gives your h and w = (area B)/h , for a blue rectangle at 45°.
Superpowacow

0

"maybe yes, but you still write "rotation 38° " , I guess it is more now," .....but I would like the long sides of B to stay 39° degres after widening the ratio. Could this be why I am getting a bad result? If I am calculating the 45 degree angle this is how the formula for h would look like for me + result https://imgur.com/IhKFEAN
- M F H
  
  0
  
  I don't understand. Once you choose the angle and the surface of B, the rectangle B is entirely determined by the constraint that its corner touches the border. Your drawing looks wrong -- I don't think you get that rectange (i.e., that value of h and w) for alpha = 45° => tan = 1 => W (in the formula) := H.
- M F H
  
  0
  
  if you want ⍺ = 45° ⇒ tan ⍺ = 1 ⇒ ("fake") W = H = 768 , D = 768 √2 = 1086.12 ⇒ h = ½ 1086.12 ∙ [ 1 ± sqrt( 1 − 4 ∙ 120'000 / 1086.12² )] = 124.8, w = 120'000/h = 961.3
- M F H
  
  0
  
  Re-3 : I didn't see you put the data, at first. Now I see that the problem was the value of D that wasn't changed according to the new W. With D = sqrt(W²+H²) = H sqrt 2 for 45°, you'll get the correct result.
M F H

0

Oh sorry, for 45° it doesn't matter, but for other alpha it must be W = H / tan alpha, not "times" (*) as I wrote in my first reply yesterday. PS: also updated the HTML page, see at bottom.
- Superpowacow
  
  0
  
  Ah yes, thank you for the fast replies !!! I noticed my mistake later on. But I am still having troubles making it work for different angles besides 45°. These are the values I get when I calculate for 44° + result (https://docs.google.com/document/d/1fiWn2saCv86maej2J-mSbXvOAdMRQI-CdhZXJAVVMNk/edit?usp=sharing) Could you please point out where the culprit might be ? (I used CAD program so the drawing should be accurate...I hope) Thank you again for bearing with me ..... : - D
M F H

0

You must use –(sqrt-part). h should be the smaller value (the "thickness" of B, w the larger one (the "length", which I called "width" in analogy of that of A)
Superpowacow

0

Oh I see, I actually tried both options haha, but it did not show up in the program I was using. With the CAD it works !!! Although, I see that I am also getting computation issues and getting imaginary numbers for the lower angles below 30°. But still now I tried a bit lower angle 37° to avoid that problem and I still unfortunately get this: ((https://docs.google.com/document/d/1fiWn2saCv86maej2J-mSbXvOAdMRQI-CdhZXJAVVMNk/edit?usp=sharing)) Is it again just on my end?
- M F H
  
  0
  
  you left an "old" value for D, I get 768 * sqrt(1+tan(37°)^2) = 1306.6 ... I guess you should write a small Python (or whatever) program (or a spread sheet...) that asks for the angle alpha and then computes and prints all the values.
M F H

0

here you go : https://docs.google.com/spreadsheets/d/1zfVkwbrCWWu4_yziHGEG2q3muxwzgDSP2Tm6suVni-g/edit?usp=sharing
Superpowacow

0

Oh I see! That is a good idea ... I tried doing that with Processing (that's where my main project is) but I found out that since it does not give all the numbers behind the decimal point it gave me errors with some angles. So I used wolframalpha. I gave a python a go and it also does not give as big precision, but I suppose there is way..., but doing that I noticed my value is different because I did not exponentiate the 1 !!! When I put in 768 * sqrt(1+tan(37°)^2) = 961.640.....
- Superpowacow
  
  0
  
  .....so that has been probably the issue ....So thank you so much for the excel sheet and swift support (I needed this for my upcoming art exhibition) !!! I gave it a few tries and it seems to be working flawlessly!!!
M F H

0

Thanks for the tip. If that would help I can give you Python code. (I don't think precision should be an issue, it should have 16 correct decimals, so ... even with an enormous zoom of like factor 1000 000, there should be no "error" perceptable for the eye.

$Calculating aspect ratio limits of rotated rectangle within a rectangle$

Answer

Related Questions

Search