Geometry without using trigonometry
So I'm supposed to find the area of the blue figure without using trigonometry. What do I have to do to find this?
Noobis
Answer
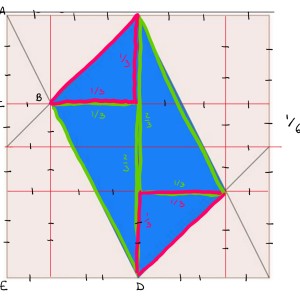
Look at the attached picture. We have that the triangles $ABC$ and $ADE$ are similar, so since $AE = 2AD$ then $AC = 2AB$. Now since there are so many right angles, all the segments marked with a single tick have the same length, and the ones marked with two ticks have twice that length. It follows that, if the big square has side lenght equal to $1$, then $AB = 1/6$. Now we can split the blue figure in four triangles, whose areas are easy to calculate: the green ones have area $1/9$, the pink ones $1/18$. Putting all those together, the area of the blue figure is \[ 2 \cdot \frac{1}{ 9} + 2 \cdot \frac{1}{18} = \frac{3}{9} = \frac{1}{3}. \]
Alessandro Iraci
-
I obviously meant BC instead of AB and DE instead of AD, but I guess you figured it out!
- answered
- 2483 views
- $5.89
Related Questions
- Geometric Representation Problem
- Probability that the distance between two points on the sides of a square is larger than the length of the sides
- Help Calculating Surface Area of a Cylinder with a Slit
- Geometry Problem about Hole Placement on PVC Pipe
- Figure 1 shows two points A and B with a straight line drawn through them.
- Find the volume of the solid obtained by rotating $y=x^2$ about y-axis, between $x=1$ and $x=2$, using the shell method.
- Find the Curvature of Parabolic Wave
- Land area calculation/verification
Low bounty! Your deadline is also too short.
I think there's some missing info? Do the diagonal lines pass through the middle points of the edges of the square?