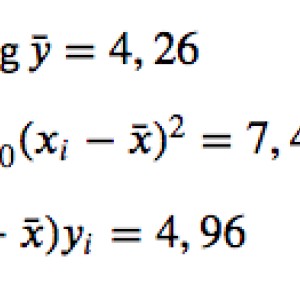Statistics tasks
An analytician is studying the profits of a company over the course of ten years. Let X be the number of years after the inital year the analytician is studying. Y is the profits in year X and the analytician believes the profits are a normal distribution stochastic(random) variable with expectation 𝐸(𝑌)=𝛽0+𝛽1𝑥 and standard deviation 𝜎=0.08. Based on these observations the analytician finds that:
𝑥¯=3.6 and 𝑦¯=4.26
𝑀=∑^9_𝑖=0 (𝑥𝑖−𝑥¯)^2=7.44,
∑^9_𝑖=0 (𝑥𝑖−𝑥¯)𝑦𝑖=4.96
(I added this as a picture too as I have a hard time writing formulas on here)
Questions:
1. Estimate 𝛽0 og 𝛽1.
2. Can it be proven that the yearly increase in profits, 𝛽1, is bigger than 0.5? Formulate fitting hypothesis and do a hypothesis test at 0,5% significance level.
Critical value=
H1 or not H1?
3.Find a 99% confidence interval for expected profits for x=5
Upper confidence limit:
Lower confidence limit:
4. Find a 95% prediction interval for expected profits for x=1
Upper prediction limit:
Lower prediction limit:
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
- answered
- 1561 views
- $5.41
Related Questions
- What is the normal probability distribution function?
- Statisitical Experimental Design Question
- Figuring out the maths for the probability of two adopted teens randomly being matched as pen pals in 2003
- Combinations of factors not observed, non-full rank design matrix. How to explain to investigator?
- Quantitative reasoning
- Relative percentage increase / decrease
-
Rolling dice statistics, probability of rolling a straight
- How do you calculate per 1,000? And how do you compensate for additional variables?