Leaky Buckets: Volume in a system of 2+ buckets that can be empty

Let us first state some more or less obvious facts.

1°) A bucket loses volume if and only if the inflow (from all other buckets) is strictly less than its (fixed, maximum) outflow. In particular this is the case if a bucket that was nonempty for $0 < t < t^*$ becomes empty at some time $t^* > 0$.

2°) An initially empty bucket can become nonempty right at the start, if the inflow from the other buckets is larger than its maximum outflow.

3°) No bucket that previously became or remained empty at some time t* > 0, can ever become nonempty at some time $t > t^*$. Indeed, assume that this happens for the first time at some $t' > t^*$, for some bucket(s) number $ i_1, …, i_k $. It can only happen if the inflow of bucket(s) $i_1, …, i_k$ had increased beyond their (fixed maximum) outflow rate, but that isn't possible unless some other bucket(s) became nonempty just before, in contradiction with the definition of $t'$ and $i_1, …, i_k$. (The increased inflow cannot come from the buckets $i_1, …, i_k$ themselves, since if this were possible, it should have happened already earlier, as by assumption at any moment the maximum possible outflow is pumped out of each bucket.)

4°) We conclude that for each bucket number $i$ there is a time $t_i \in [0,\infty]$ such that
$W_i(t) > 0 \iff 0 < t < t_i$, and $W_i(t) = 0 \iff t \ge t_i$.
(Then $t_i = 0$ means that the bucket is always empty, and $t_i = \infty$ means the bucket is nonempty for all $t>0$.)

5°) In general the system reaches an equilibrium state with $m$ empty buckets and $N-m \ge 1$ buckets that remain nonempty forever. These are in general the buckets with the smallest (maximum) outflow rate; those with a larger outflow rate (and also the source bucket) will eventually become empty.

6°) For later it will be more convenient to reorder the indices according to when the buckets become empty:
$ \{  t_0, t_1, …, t_{N-1} \} = \{ t_{i_1}, t_{i_2}, …t_{i_{N}} \}$ with $0 =: t_{i_0} \le t_{i_1} \le …\le t_{i_m} < t_{i_k} = \infty$ for all $k > m$, where $m$ is the number of buckets that become empty at some moment.
(Unless all buckets are empty at the beginning and forever, there will always remain at least one bucket nonempty forever, since no water is ever lost but only pumped from one bucket into another one: see also 14° at the end.)
To simplify notations, let's also define the corresponding time intervals $ I_k = [t_{i_{k-1}} , t_{i_{k}}]$.
(We'll see below how these $t_i$ are actually computed!)

7°) It will be handy to define the functions which give the flow from a given bucket $i$ to each other (non-source) bucket:
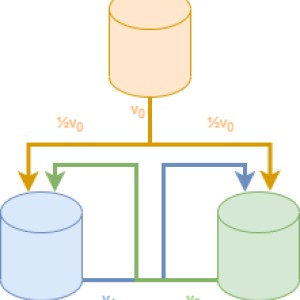
$ u_0(t) := [~v_0 / (N-2) ~$ if $~ W_0(t)>0 ~$ else $~ 0 ~] $, and
$\forall i > 0 : u_i(t) := [~ v_i~$ if $~ W_i(t) > 0 ~$ else $~ \min\{ v_i, \sum_{j \ne i} u_j(t) \} ~] / (N-1) $
These definitions are crucial and the basis for all subsequent computations. They should be clear: when a bucket is nonempty, its outflow is given by $~v_i~$, to be distributed over all other receiving buckets. When it's empty, its outflow is not zero but equal to the minimum of $~v_i~$ and the sum of the inflow coming from all other buckets. Actually, that  minimum should always be that sum of the inflows, meaning that all that comes in will instantly be pumped out, so that the bucket remains empty. If the bucket was initially empty, it is possible that the inflow is larger than the maximum outflow (see 2°), but then the bucket will immediately become nonempty.  

8°) Then the "volumes" satisfy the following differential equations:
* $ W'_0(t) = - v_0 ~$ while $~ W_0 > 0 $, i.e., for $ 0 \le t < w_0 / v_0 $, and 0 otherwise.
* $\forall i > 0:~ W'_i(t) = [ \sum_{j \ne i } u_j(t)~ ] - v_i ~$ if $~ W_i(t) > 0 ~$ (and otherwise, $\forall t>0:W_i(t)=0 ~\Rightarrow~W'_i(t)=0$).
(But as we'll see below, these derivatives are not well defined in a few points $t_{k}$ in which one may have $~W'_i(t_k^-) \ne W'_i(t_k^+)$, where $f(t^\pm) := \lim_{h\to 0^+} f(t\pm h)$. So in general it will either be clear inside which interval $I_k$ is $t$, or we'll make explicit whether $t$ is to the right or to the left of a given $t_k$.)

Obviously, the first equation is easy to integrate over all time:
$ W_0(t) = \max( w_0 - v_0 \, t , 0 ) = [~w_0 - v_0 \, t ~$ if $~ 0 \le t < w_0/v_0 ~$ else $~0~]$.
For the others, it is more complicated, because their inflow depends on the other sources and in particular, whether they are empty or not at a given moment.

9°) Within the interior of the time intervals $I_k = [t_{i_{k-1}} , t_{i_{k}}] $, where no bucket becomes empty, all flows $u_i(t)$ and $W'_i(t)$ are constant (so the argument $t$ is only needed to know in which interval $I_k$ the constant is taken), and a bucket that has $W_i(t^*) > 0$ at some time $  t^* \in I_{k}^\circ $ will satisfy the equation $W_i(t) = W_i(t^*) + W'_i(t^*) (t-t^*)$ (which is a straight line of constant (usually negative) slope $W'_i(t)$ given in 8°) for all $t\in I_k$, up to the moment $t_{i_{k}}$ where some bucket becomes empty.

10°) At a given moment $t$, if nothing changed, such a bucket would become empty after a time
$\Delta_i(t) := -W_i(t) / W'_i(t)$, if this is a finite positive number.
Otherwise (for buckets that are already empty or have inflow $\ge$ outflow), we let $\Delta_i(t) = \infty$.
Then the next change will occur after a lapse of time $\Delta(t) := \min\{\Delta_i(t) ; i \ge 0 \}$.
Usually, we would compute $\Delta_i^{(k)} = \Delta_i(t_{i_{k-1}}^+) $  at the beginning = to the left of the interval $ I_k $, and their minimum
$\Delta^{(k)} = \min \{ \Delta_i^{(k)} ; 0 \le \Delta_i^{(k)}<\infty \} $: this is exactly the length of the interval $I_k$, and it determines $t_{i_{k}} = t_{i_{k-1}} + \Delta^{(k)}$.
(An interval of length 0 means that bucket $i_k$ went empty at the same time than the preceding bucket.)

11°) Then, the next change will occur at  $ t_{i_{k}} = t_{i_{k-1}} + \Delta^{(k)} $, unless $k = m \iff \Delta(t) = \infty \iff$ the system has reached its equilibrium state, and nothing will change any more: $~\forall i \ge 0,~ \forall t' > t_{i_m}:~ W_i(t') = W_i(t)$.

12°) If $~k < m~$, then at time $~ t + \Delta(t)~$, the buckets with $~\Delta_i(t) = \Delta(t)~$ will become empty,
and their outflow will drop from $~v_i~$ to what they receive (for $i>0$) from the others,
$~\sum_{j\ne i}u_i(t)~$ (which is necessarily less than $ v_i $, since otherwise $~\Delta_i = \infty~$).

13°) So we finally have the following solutions:
$W_{i_1}(t) = W_{i_1}(0) + W'_{i_1}(0^+)\,t~$ for $~0 \le t \le t_{i_1} = \Delta^{(1)} = \Delta_{i_1}(0^+)~$
(this defines $~i_1$: the index of the smallest positive $\Delta_{i}(0^+)$ as defined in 10°),
and $~\forall t>t_{i_1}:~W_{i_1}(t) = 0~$.

Next we have:
$W_{i_2}(t) = W_{i_2}(0) + W'_{i_2}(0^+)\,t~$ for $~0 \le t \le t_{i_1}~$, and
$W_{i_2}(t) = W_{i_2}(t_{i_1}) + W'_{i_2}(t_{i_1}^+)\,(t-t_{i_1})~$ for $~ t_{i_1} \le t \le t_{i_2} :=  t_{i_1}+\Delta^{(2)}~$,
and $~\forall t>t_{i_2}:~W_{i_2}(t) = 0$.

And so on. The last one that gets empty at some point is
$~W_{i_m}(t) = W_{i_m}(0) + W'_{i_m}(0^+)\,t~$ for $~0 \le t \le t_{i_1}~$,
$~W_{i_m}(t) = W_{i_m}(t_{i_1}) + W'_{i_m}(t_{i_1}^+)\,(t-t_{i_1})~$ for $~ t_{i_1} \le t \le t_{i_2}$,
…
$~W_{i_m}(t) = W_{i_m}(t_{i_{m-1}}) + W'_{i_m}(t_{i_{m-1}}^+)\,(t-t_{i_{m-1}})~$ for $~ t_{i_{m-1}} \le t \le t_{i_m} :=  t_{i_{m-1}}+\Delta^{(m)}~$,
and $~\forall t \ge t_{i_m}:~W_{i_m}(t) = 0$.

Unfortunately, there is no simpler formula than that for these piecewise defined functions.

I have made a google sheet that allows make numerical simulations and see how the successive $\Delta^{(k)}$ and $t_{i_k}$ are computed: https://docs.google.com/spreadsheets/d/1giKGtubTUGkyISBwmf0vK8vpPyAyLI845gUavyaCVIY/edit#gid=0

14°) Concerning the final equilibrium state, for $t \ge T := t_{i_m}$, we have
$\forall k>m:~\forall t>T: W_{i_k}(t) = W_{i_k}(T) ~$,
and the sum of these constant nonzero volumes is the same as the sum of all initial volumes,
$~\sum_{k>m} W_{i_k}(T) = \sum_{i\ge0}W_i(0)~$,
and the inflow and outflow of all of the (non-source) buckets, empty or not, is equal to the smallest such flow rate, $ v^* = \min\{ v_i \mid i>0\} $ (assuming that all of them are positive).