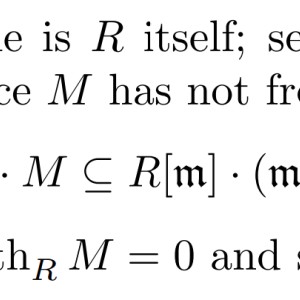Length of finitely generated module over $0$-dimensional Gorenstein local ring
Please see attached images: Can someone slowly walk me through the details of the proof of Lemma 4.1 using basic commutative algebraic arguments and definitions?
1) Why $R[\mathfrak{m}] \cong k$? (where $k$ is the residue field of $R$)
2) I know length is additive on direct sums, but how is the RHS of the inequality additive as well, since it is a product?
3) Why does the inequality coincide when $R$ is the module over itself?
4) How does $R$ being Gorenstein of dimension $0$ imply that $R$ is the only indecomposable injective module, and why is its injective hull free as a result?
5) Why $M \subseteq \mathfrak{m}F$?
6) Why does $M=0$ imply the desired result?
Jbuck
152
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- closed
- 1433 views
- $44.00
Related Questions
- Let $R$ be an integral domain and $M$ a finitely generated $R$-module. Show that $rank(M/Tor(M))$=$rank(M)$
- Vector field
- Abstract Algebra : Commutativity and Abelian property in Groups and Rings
- How do you go about solving this question?
- Question on a subgroup of permutations
- Stuck on this and need the answer for this problem at 6. Thanks
- Let $f(x,y,z)=(x^2\cos (yz), \sin (x^2y)-x, e^{y \sin z})$. Compute the derivative matrix $Df$.
- Algebra Word Problem #1
