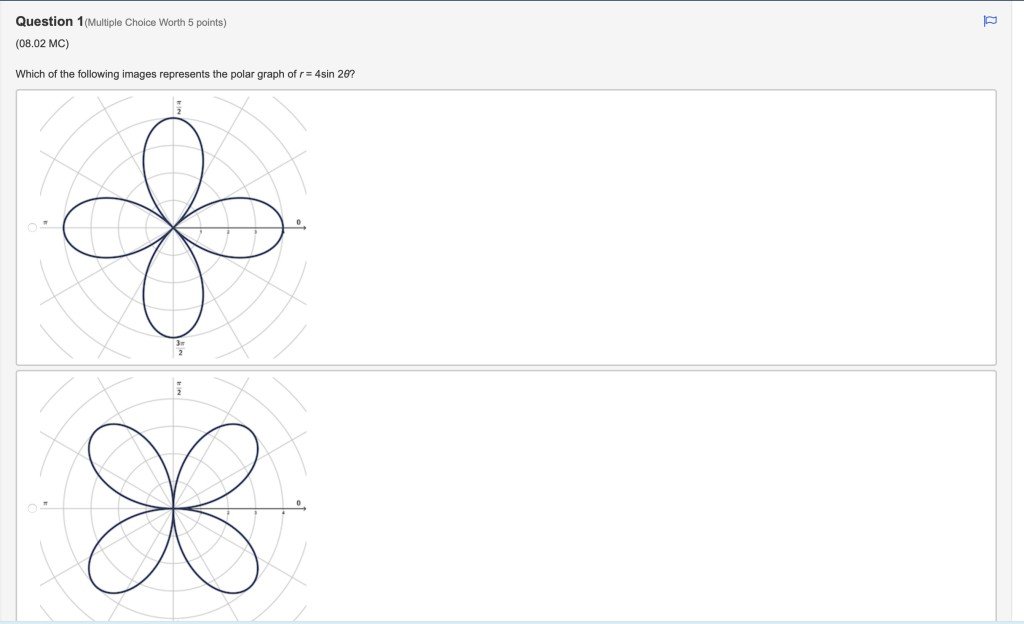
Q 1:
Answer is the second graph.
$r=asin(nθ)$ is a rose with radius a and 2n petals for even number n.
---------------------------------------------------------------------------------------------------------------------
Q2:
Answer is choice 2.
$t=x-2$
$y=(x-2)^{2} +3(x-2)$
$y=x^{2} -x-2 $
---------------------------------------------------------------------------------------------------------------------
Q3:
Answer is choice 3.
$V1=58 ft/s \times cos(19^{^{\circ} } )=54.84 ft/s$
$V2=58 ft/s \times sin(19^{^{\circ} } )=18.89 ft/s$
....
---------------------------------------------------------------------------------------------------------------------
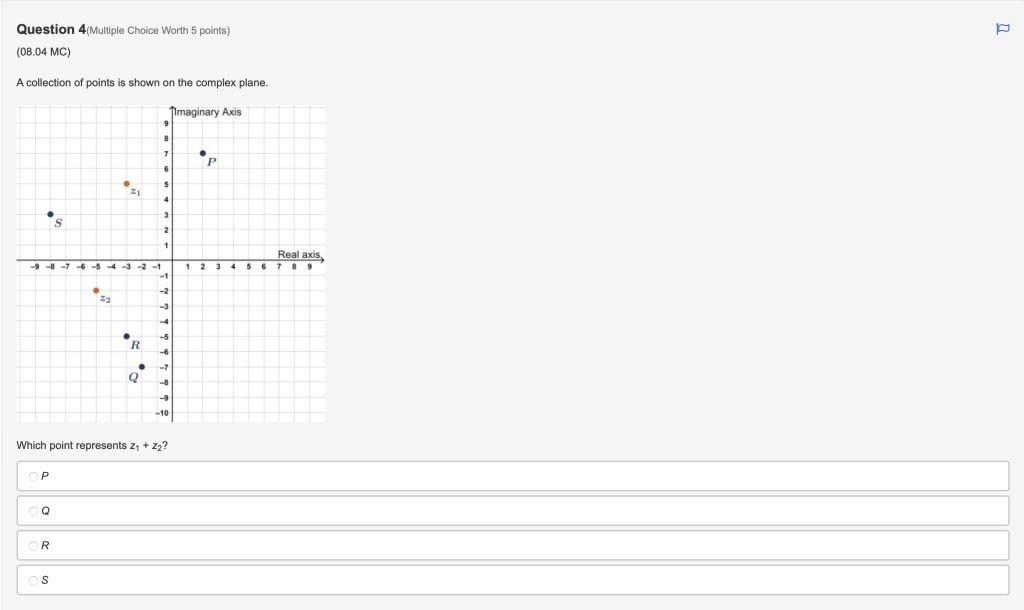
Q4:
Answer is choice 4.
---------------------------------------------------------------------------------------------------------------------
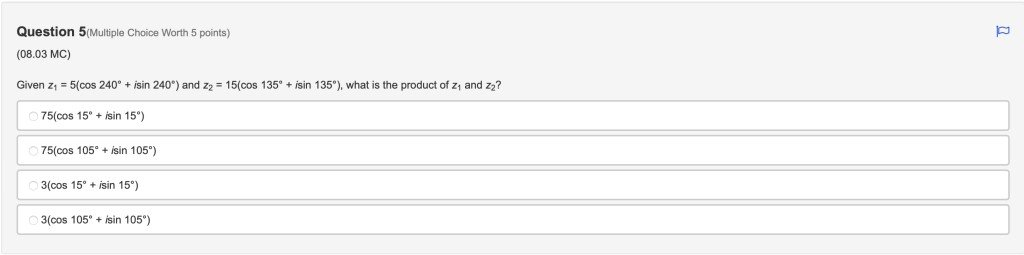
Q5:
Answer is choice 1.
Convert the angles to radians:
$\frac{240\pi }{180}$
$\frac{135\pi }{180}$
Then, calculate the trigonometric functions:
$cos(\frac{240\pi }{180})≈−0.5 $
$sin(\frac{240\pi }{180})≈−0.8660 $
$cos(\frac{135\pi }{180})≈-0.7071 $
$sin(\frac{135\pi }{180})≈0.7071 $
So, we have:
$5\times 15=75$
$cos(375^{^{\circ} } )=cos(360^{\circ} +15^{\circ} )$
...
---------------------------------------------------------------------------------------------------------------------
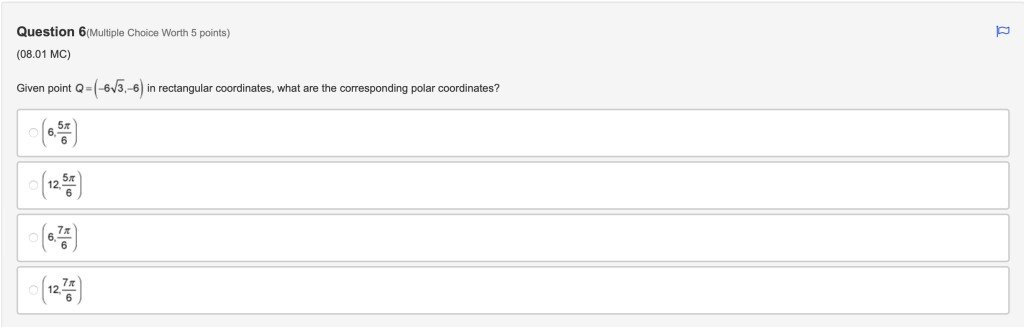
Q 6:
Answer is choice 4.
$r=\sqrt{(-6\sqrt{3} )^{2}+(-6)^{2}} =12 $
$rcosθ=-6\sqrt{3} $
$rsinθ=-6 $
$cosθ=-6\sqrt{3}/12=\frac{-\sqrt{3} }{2} $
$sinθ=\frac{-6}{12} =\frac{-1}{2} $
$θ=\frac{7\pi }{6} $
---------------------------------------------------------------------------------------------------------------------
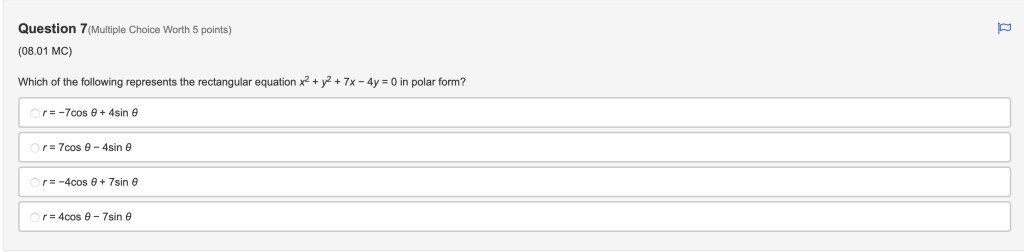
Q7:
Answer is choice 1.
Assume:
$x=rcosθ $
and
$y=rsinθ$
$x^2+y^2+7x-4y=0 $
$r^2+7rcosθ-4rsinθ=0 $
$r=-7cosθ +4sinθ$
---------------------------------------------------------------------------------------------------------------------
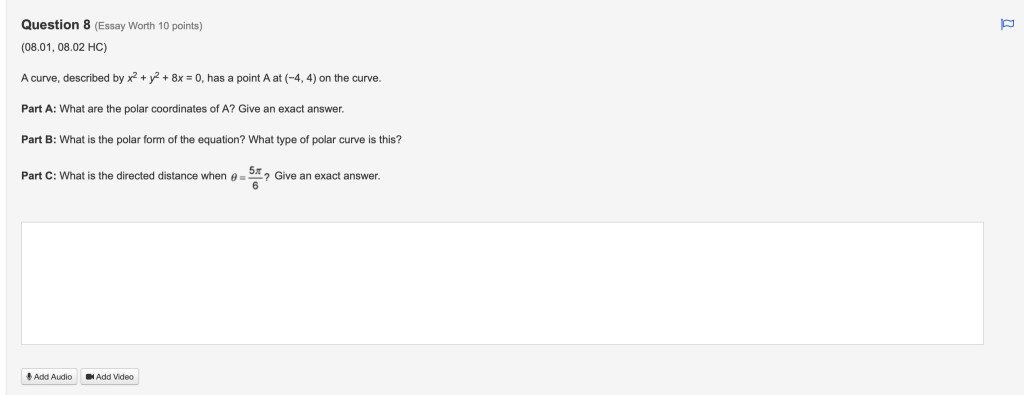
Q8:
Assume:
$x=rcosθ $
and
$y=rsinθ$
point A: (-4,4), so, we have:
$-4=rcosθ$
and
$4=rsinθ$
So, we have:
$-4/r=cosθ$
$4/r=sinθ$
We have:
$sin^2(θ)+cos^2(θ)=1 $
So:
$(-4/r)^2 + (4/r)^2=1$
So:
$r=4$\sqrt{2}$
$θ=\frac{3\pi }{4}$
$A(θ,r)=A(\frac{3\pi }{4}, 4\sqrt{2}) $
------------------------------
$x^2+y^2+8x=0$
$x^2+y^2=8x$
$(rcosθ)^2+(rsinθ)^2=-8rcosθ$
$r=-8cosθ$
The polar curve is circle.
------------------------------
$θ=\frac{5\pi }{6}$
$r=-8cos(\frac{5\pi }{6})$
$=-8\times \frac{-\sqrt{3} }{2} =4\sqrt{3} $
---------------------------------------------------------------------------------------------------------------------
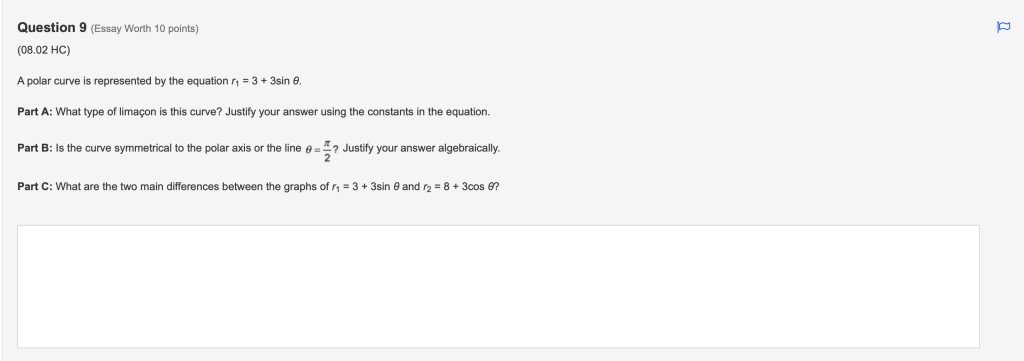
Q9:
Because a/b = 3/3 = 1, the limacon is a cardiod and is heart shaped.
------------------------------
Assume two angles α1 and α2 symmetrical around θ = Pi/2.
Let $α1 = \frac{\pi }{2} + x$
and
$α2 = \frac{\pi }{2} – x$
Using sum of angle formula for sine:
$sin α1 = (sin\frac{\pi }{2} )(cos x) + (cos\frac{\pi }{2})(sin x) = cos x$
$r1 = 3 + 3sinθ = 3 + 3cosθ$
sin α2 = (sin Pi/2)(cos x) - (cos Pi/2)(sin x) = cos x
$r2 = 3 + 3sinθ = 3 + 3cosθ$
Therefore, since r1 = r2, the curve is symmetrical about θ = Pi/2
------------------------------
The first equation represents a limacon that is a cardiod (heart shaped). It is symmetrical about θ = Pi/2.
The second equation, a = 8, b = 3; a/b = 2.67 (>2). Therefore, the plot of this equation is a limacon with no dimple and no inner loop. And since the equation is a cosine, it’s symmetrical about the polar axis.
---------------------------------------------------------------------------------------------------------------------
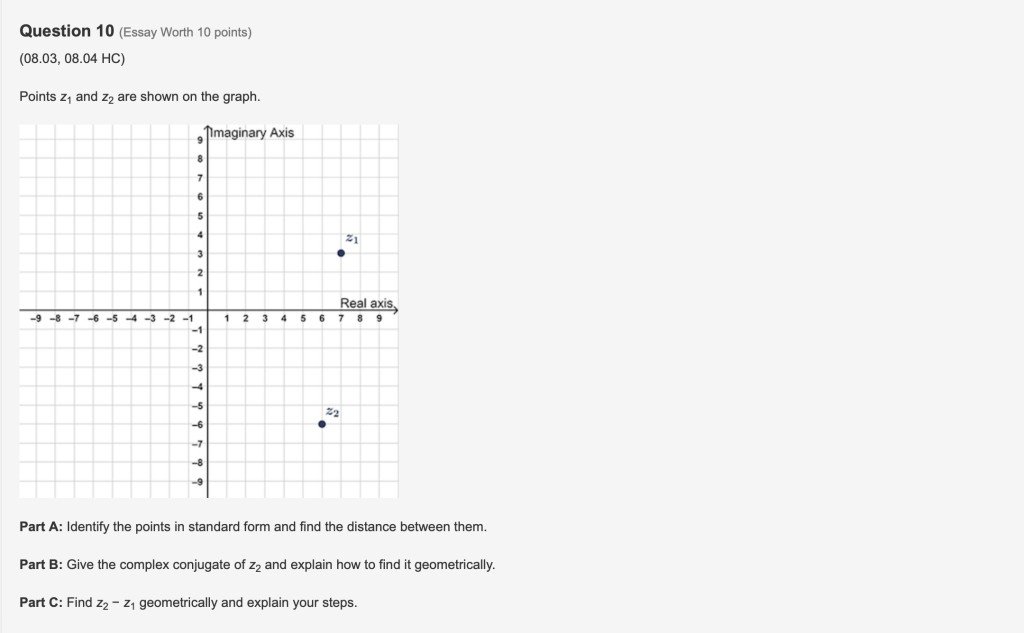
Q10:
The point z1 is at (7,3) and the point z2 is at (6,-6).
Distance between them:
$D=\sqrt{(7-6)^2+(3-(-6))^2} =9.05 $
Coordinates of Z2 are (6,-6), so:
Complex conjugate to z2:
$z2=6-(-6)i=6+6i $
To find it geometrically,we reflect point z2 across x-Axis.
We know that z2-z1=(Real part of z2-Real part of z1)+i(imaginary part of z2-imaginary part of z1), so, to find z2-z1 geometrically:
Move z2 to the left 1 units (real part of z2 - real part of z1). Then, move z2 down 3 units (imaginary part of z2-imaginary part of z1). The new z2 is z2-z1.
---------------------------------------------------------------------------------------------------------------------
Q 11:
Part A: The ordered pairs (x, y) when t = 0.2, 1.2, and 2.2 are (27, 10.26), (162, 25.86), and (297, 10.74) respectively.
Part B: The baseball does not clear the 10-foot tall fence located 320 feet away from home plate.
Part C: The rectangular equation to represent the plane curve is $y = 3.3 + 38x - 16x^2$.
Part A: Substitute the given values of t into the equations $x = 135t$ and $y = 3.3 + 38t - 16t^2$.
For t = 0.2:
$x = 135 * 0.2 = 27, y = 3.3 + 38 * 0.2 - 16 * (0.2)^2 = 10.26$
So, (x, y) = (27, 10.26).
For t = 1.2:
$x = 135 * 1.2 = 162, y = 3.3 + 38 * 1.2 - 16 * (1.2)^2 = 25.86$
So, (x, y) = (162, 25.86).
For t = 2.2:
$x = 135 * 2.2 = 297, y = 3.3 + 38 * 2.2 - 16 * (2.2)^2 = 9.46$
So, (x, y) = (297, 9.46).
Part B: Substitute the x-coordinate of the fence (320) into the equation for y and if the resulting value is greater than 10, then the baseball clears the fence.
So, we get:
$y = 3.3 + 38 * 2.37- 16 * 2.37^2 = 3.49 <10$
Since the resulting y-coordinate is less than 10, the baseball does not clear the fence.
Part C: The rectangular equation to represent the plane curve is y = 3.3 + 38t - 16t^2.
Replacing t=x/135, we have:
$y = 3.3 + 38(x/135) - 16(x/135)^2$


 Kav10
Kav10

In the rubric questions 1 2 3 4, denotes for question 8,9,10,11. Thanks
Hey Nicolas. I am gonna get started now. Would you be able to extend the deadline?
I can, but would you finish ASAP, there technically no limit, but I just wanna check my answer.
Yes. I have already started. I will let you know.
I don't need steps for MCQ, just for the written ones
How's it going?
Just finishing up. One question is remaining. So many parts!
I am gonna submit what I have so far, so you can start checking. Then, will work on the remaining and update. Sounds good?
For the last one I got this, (I used my phone to transfer so it's kinda weird) Part A: Problem: Find the ordered pairs (x, y) for the baseball's path when t = 0.2, 1.2, and 2.2. Solution: For t = 0.2, using x = 135t and y = 3.3 + 38t - 16t^2: x(0.2) = 135 * 0.2 = 27 y(0.2) = 3.3 + 38 * 0.2 - 16 * (0.2)^2 = 3.3 + 7.6 - 0.64 = 10.26 For t = 1.2: x(1.2) = 135 * 1.2 = 162 y(1.2) = 3.3 + 38 * 1.2 - 16 * (1.2)^2 = 3.3 + 45.6 - 23.04 = 25.86 For t = 2.2: x(2.2) = 135 * 2.2 = 297
y(2.2) = 3.3 + 38 * 2.2 - 16 * (2.2)^2 = 3.3 + 83.6 - 77.44 = 9.46 Final Answer for Part A: The ordered pairs are (27, 10.26) at t = 0.2, (162, 25.86) at t = 1.2, and (297, 9.46) at t = 2.2. Part B: Problem: Determine if the baseball goes over the fence that is 10 feet tall and 320 feet away from home plate. Solution: Find the time t when x = 320 by using x = 135t: 320 = 135t t = 320 / 135 t ≈ 2.37 Now, use this t value to find the height y: y(2.37) = 3.3 + 38 * 2.37 - 16 * (2.37)^2 y(2.37
y(2.37) = 3.3 + 38 * 2.37 - 16 * (2.37)^2 y(2.37) = 3.3 + 89.86 - 89.58 y(2.37) ≈ 3.58 Final Answer for Part B: When the baseball is 320 feet away from home plate, its height is approximately 3.58 feet, which is below the fence height of 10 feet. Therefore, the baseball does not go over the fence. Part C: Problem: Convert the parametric equations to a single rectangular equation for the curve.
Solution: We have the parametric equations x = 135t and y = 3.3 + 38t - 16t^2. To eliminate the parameter t and write the equation in rectangular form, we express t in terms of x: t = x / 135. Now, substitute t with x / 135 in the equation for y: y = 3.3 + 38(x / 135) - 16(x / 135)^2 To simplify, multiply each term by the corresponding power of 135 to eliminate the fraction: y = 3.3 + (38/135)x - (16/135^2)x^2
y = 3.3 + (38/135)x - (16/135^2)x^2 Simplify the equation for y to get the rectangular form. Final Answer: The rectangular equation for the curve is y = 3.3 + 38x/135 - 16x²/18225, after simplification.