$Understanding Cylindrical Warping Equations and Derivation$

Question

$Understanding Cylindrical Warping Equations and Derivation$

Hello,

I would really appreciate some help understanding the derivation for x' and y' for Equation (1), Equation (2), and Equation (3).

I recall that to convert Cylindrical Coordinates to Cartesian Coordinates it would be x = r × cos(⊖), y = r × sin(⊖), z = z. Also, to convert Cartesian Coordinates to Cylindrical Coordinates it would be r^2 = x^2 + y^2, ⊖ = arctan(y/x), z = z.

Here is a link to the article I was reading: https://arxiv.org/abs/1803.06655

Also, is the focal length, f supposed to be the radius? I would also appreciate it to see how they derived Equation 1. Thank you so much!

Trigonometry Polar Coordinates Trigonometric Functions

Squareroot123

8

Matchmaticians Understanding Cylindrical Warping Equations and Derivation File #1

File #1 (jpg)

Report

Answer

The answer is accepted.

Join Matchmaticians Affiliate Marketing Program to earn up to a 50% commission on every question that your affiliated users ask or answer.

Answer 1

Answers can only be viewed under the following conditions:

The questioner was satisfied with and accepted the answer, or
The answer was evaluated as being 100% correct by the judge.

View the answer

Please see the formulas in equation (1) of the following reference:

http://szeliski.org/papers/Szeliski_FullViewPanoramicMosaics_SG97.pdf

As you see, given. $(X,Y,Z)$ in the real world its 2D cylindrical coordinate $(\theta, v)$ is defined as
\[\theta =\tan^{-1}(X/Z), v=\frac{Y}{\sqrt{X^2+Z^2}}.\]

Note that $\theta$ is measured from $z$, i.e. $\theta=0$ on $z$-axis (similarto how it is defined in polar coordinates). The paper is poorly written and it shows that $\theta$ is measured from $x$ axis which is not correct.Also $v$ represents the slope that the line segment from the origin to $(X,Y,Z)$ makes with $xz$-plane. Note that these two quantities represent angles. Indeed one can define $\varphi = \tan^{-1}(\frac{Y}{\sqrt{x^2+Z^2}})$.

Since the focal length is $f$, i.e. an square of length 1 is mapped to a square of length $f$. Thus all angles should be multiplied by $f$, and hence for the point $(x,y,f)$ you get
\[\theta =\tan^{-1}(x/f), v=\frac{y}{\sqrt{x^2+f^2}}.\]
So
\[x'=f \theta =f \tan^{-1}(x/f), y'=vf=f\frac{y}{\sqrt{x^2+f^2}}.\]

If the center of the cylinder is $(a,b)$ instead of $(0,0)$ one can shift the whole system from $(a,b)$ to $(0,0)$ by a the change of variable $\tilde{X}=X-a$, and $\tilde{Y}=Y-a$. So the formulas in (2) and (3) are just (1) under this change of variable. We replace $x$ by $x-a$, $y$ by $y-b$, $x'$ by $x'-a$, and $y'$ by $y'-b$:
\[x'-a= f \tan^{-1}((x-a)/f), y'-b=vf=f\frac{y-b}{\sqrt{(x-a)^2+f^2}}\]
\[\Rightarrow x'=f \tan^{-1}((x-a)/f)+a, y'=vf=f\frac{y-b}{\sqrt{(x-a)^2+f^2}}+b.\]

This sounded like a simple problem at first, but took me a while to figure out. I would appreciate a tip!

1 Attachment

Erdos

4.8K

Erdos

+1

Let me know if you need any clarifications.
- Squareroot123
  
  0
  
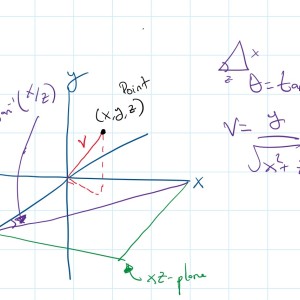
  Hi Erdos, thanks for your help. I'm still confused about the position of x,y,z in the real world. Can you draw a graph? Also, just to confirm v is an angle as well? Also, can you talk more about the focal length?
Squareroot123

0

Hi again, Erdos, also I wanted an explanation regarding Equation (2) and Equation (3) of my post as well. Thanks!
- Erdos
  
  +1
  
  I added more details about (2) and (3).
Squareroot123

0

Hi Erdos, I have added a file where I'm trying to draw visualize the equations - This relates to my first reply
Erdos

+1

See the graph in the attached file.
- Squareroot123
  
  0
  
  Thanks, Erdos! That was extremely helpful!
Squareroot123

0

Erdos, I promise that I will provide you a tip! May you please explain: Since the focal length is f, i.e. an square of length 1 is mapped to a square of length f. Thus all angles should be multiplied by f. Also, once again, just to confirm v is an angle as well? I ask this because you state: Note that these two quantities represent angles. Once again, thank you so much!
- Erdos
  
  +1
  
  v is the slope of the line OP and not an angle, but intrinsically it represents the tangent of the angle phi i mentioned above.
Erdos

+1

The authors do not clearly define what they mean by focal length. However, in this context, it means that a point with coordinates (theta, v) is mapped to a point (f theta, f v). This means that both theta and f are expanded by a factor of f.
Squareroot123

0

Hi Erdos, apologies if you have answered this question, but why do we want to multiply the focal length to the equations you derived? Also, dumb question, but for the slope of the line P, why can't we use the Pythagorean theorem like we did for the xz-plane? Also, let's say for example that the focal length is related to a camera matrix - How does this change the problem? Thanks!
- Erdos
  
  0
  
  For the slope of the line P, we actually use the Pythagorean theorem on the triangle OPA. I don't have time to answer your other questions about the focal length. It almost requires writing a comprehensive tutorial. Please note that this problem has taken me over 1.5 hours, I am only getting paid like $16 (including the tip). This is an advanced question, and my time is too valuable to be working for lower than minimum wage.
- Erdos
  
  0
  
  If you have further questions, you can create a new post with a good and fair bounty.
Squareroot123

0

One more thing, may you add another drawing of where x' and y' would land on the graph? Thank you!

$Understanding Cylindrical Warping Equations and Derivation$

Answer

Related Questions

Search