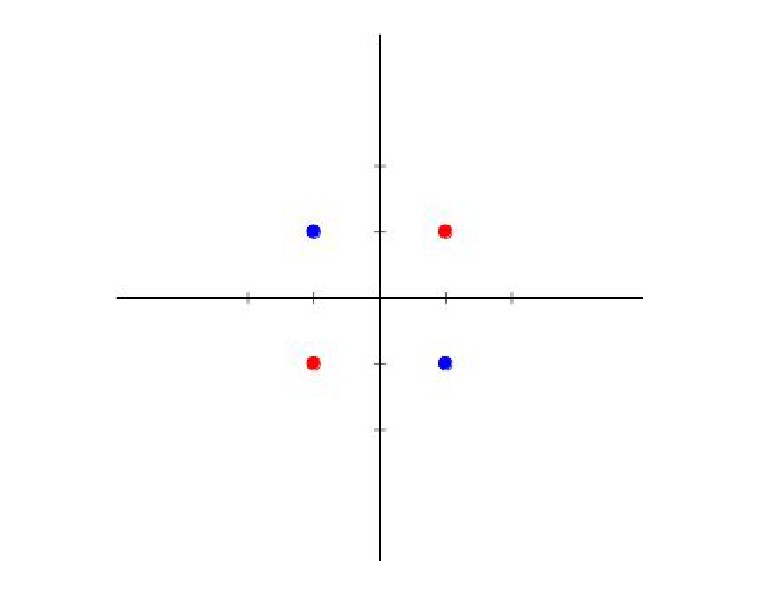
Classification problem using one or more Simple Linear Perceptron

In this exercise, we solve the following classification problem below using simple (no hidden layers) perceptrons (one or more) with two neurons at the input layer and a linear activation function.

N.B.0. : the activation function(s) MUST be linear.

N.B.1. : the colors represents whole regions rather than just a point.

N.B.2. : The solution must be done "by hand" without any implementation in R or Python and with as little calculation as possible, even without doing any calculations. The most important thing is to explain the reasoning clearly and logically, and to draw the architecture of the network(s) under consideration.

N.B.3. : Consider the tangent function, it can facilitate the resolution of this problem. (Or you may think of something else, but please try to avoid using the product function)