Consider the plane in R^4 , calculate an orthonormal basis
[Orthogonal complement in dimension 4]. Consider the plane M in R^4 defined by the following equations:
(Image 1)
(a) Calculate an orthonormal basis (v1, v2) for M
(b) Calculate an orthonormal basis (W1, W2) for the orthogonal complement of M, N= M ⊥
(c) Prove that the family β = (V1, V2,W1,W2) is an orthonormal basis for R^4
 Vienrods
Vienrods
28
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
1.7K
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1388 views
- $8.00
Related Questions
- Determinant and Inverse of a predefined matrix. The question and bounty are updated.
- [change of basis] Consider the family β = (1 + x + x 2 , x − x 2 , 2 + x 2 ) of the polynomial space of degree ≤ 2, R2[x].
- Length of a matrix module
- Questions about using matrices for finding best straight line by linear regression
- Get area of rotated polygon knowing all coordinates and angle.
- How do I evaluate and interpret these sets of vectors and their geometric descriptions?
- Linear Algebra Assistance: Linear Combinations of Vectors
- Length of a matrix module
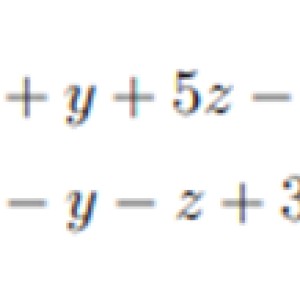

Do you need all the calculations or are you happy with the set of vectors (and the way to get them) and do the calculations yourself?
the set of vectors and how to get them is fine