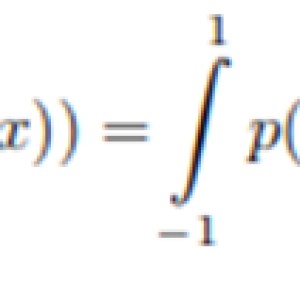Consider the function, prove that it's bilinear, symmetric, and positive definite
[Orthogonal Polynomials]. Consider the following bi-valued function defined on the space of polynomials of degree ≤ 2:
(Image 1)
For whichever polynomials p(x), q(x) ∈ P≤2. Consider the following polynomials:
p0(x) = 1, p1(x) = x, p2(x) = (3/2 )x² − 1/2 .
(a) Prove that F is bilinear, symmetric, and positive definite
(b) Prove that the family (p0, p1, p2) is an orthogonal basis of P≤2.
 Vienrods
Vienrods
28
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
1.7K
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1374 views
- $8.00
Related Questions
- Show that the $5\times 5$ matrix is not invertable
- [Linear Algebra] Proof check. Nilpotent$\Rightarrow Spec\Rightarrow$ Characteristic Polynomial $\Rightarrow$ Nilpotent
- Linear Algebra Assistance: Linear Combinations of Vectors
- How do I evaluate and interpret these sets of vectors and their geometric descriptions?
- Find the eigenvalues of $\begin{pmatrix} -1 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 3 & -1 \end{pmatrix} $
- [Linear Algebra] Spectrum
- [Rotations in R^3 ] Consider R∶ R^3 → R^3 the linear transformation that rotates π/3 around the z-axis
- Hamming metric isometries