Studying the graph of this function
I need to study the graph of this function, especially the asintotes (limits) and derivatives.
Michela
19
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
1 Attachment
Erdos
4.8K
-
Thank you! So basically x=-8 is the only asymptote ( and y=0 for the first function)? Can I also ask you how to calculate the second derivative? I can't find the concavity of the function because the second derivative is too difficult
-
x=-8 (vertical)and y=0 (horizontal) are the asymptotes. Note that lim f(x)=0 as x goes to + infinity.
-
Yes, the second derivative would be challenging. You can ask that question in a separate post.
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1819 views
- $3.94
Related Questions
- Derivatives
- Rainbow Vectors
- Is the infinite series $\sum_{n=1}^{\infty}\frac{1}{n \ln n}$ convergent or divergent?
- Relating integrals to the area under the curve using rectangles.
- Use Green’s theorem to evaluate the line integral $\int_C (1+xy^2)dx-x^2ydy$ on the arc of a parabola
- Work problem involving pumping water from tank
-
Find a general solution for the lengths of the sides of the rectangular parallelepiped with the
largest volume that can be inscribed in the following ellipsoid - Under the hood of Hard Margin SVM
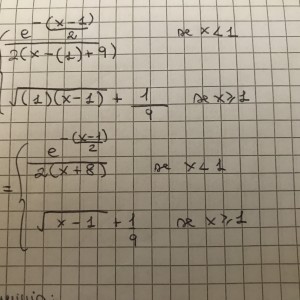
You forgot to upload the file.
thank you! I've just added it