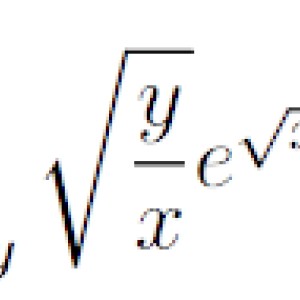Calculus Integral volume
1) Obtain the volume of the solid delimited by the elliptical paraboloid z = 10 + x^2 +3y^2 and the rectangle: 0 ≤ x ≤ 1 ; 0 ≤ y ≤ 2
2) Obtain the value of the Integral (SEE ATTACHMENT)
Kastro
27
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
1 Attachment
Aman R
649
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1229 views
- $3.10
Related Questions
- Evaluate the surface integral $\iint_{S}F \cdot dn$ over the given surface $S$
- Integration headache, please help.
- Integrate $\int_0^1\int_{\sqrt{x}}^{1}e^{y^3}dydx$
- Get the volume and surface area of the paraboloid $z=4-x^2-y^2$ cut by the plane $z=4-2x$
- Compute $$\oint_{|z-2|=2} \frac{\cos e^z}{z^2-4}dz$$
- Evaluate $\iint_{R}e^{-x-y}dx dxy$
- Calculus Questions - Domains; Limits; Derivatives; Integrals
- Integral of trig functions
