Profit maximizing with cost and price functions
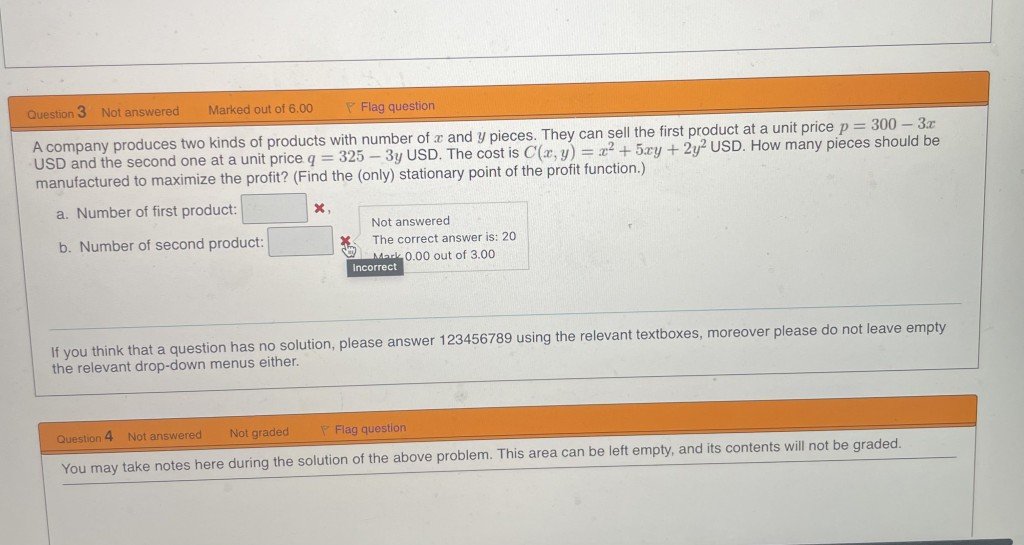
I was given the following exercise during an exam:A company produces two kinds of products with number of x and y pieces. They can sell the first product at a unit price p = 300 - 3x USD and the second one at a unit price q = 325 - 3y USD. The cost is C(x, y) = $x^2 + 5xy + y^2$ USD. How many pieces should be manufactured of each product to maximize the profit? (Find the (only) stationary point of the profit function.)
In theory, the number of first product should be 25, the number of second product should be 20. But I do not really know how they got to that solution.
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
Martin
1.5K
-
There must be a mistake on the part of the exam answer sheet, thank you for your answer!
-
Let me edit the answer with the correct cost function
-
-
Oh, I see my mistake, I am terribly sorry for the inconvenience.
-
no problem
-
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 403 views
- $5.00
Related Questions
- Calculus problems
- Find the composition function $fog(x)$
- A telephone line hanging between two poles.
- Prove that $\int_{-\infty}^{\infty}\frac{\cos ax}{x^4+1}dx=\frac{\pi}{2}e^{-\frac{a}{\sqrt{2}}}(\cos \frac{a}{\sqrt{2}}+\sin \frac{a}{\sqrt{2}} )$
- Calc limit problem
- Compute $\lim _{n \rightarrow \infty} \frac{1}{n}\ln \frac{(2n)!}{n^n n!}$
- You have a piece of 8-inch-wide metal which you are going to make into a gutter by bending up 3 inches on each side
- Business Calculus. Finding the deriviative.
Are you sure the numbers in the question are accurate?
I am 100% sure, I'd send you pictures of the exercise and the supposed correct answer (just the end result), but I cannot.
The cost function is not correct then.