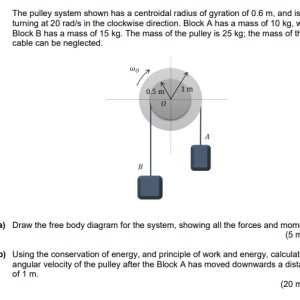
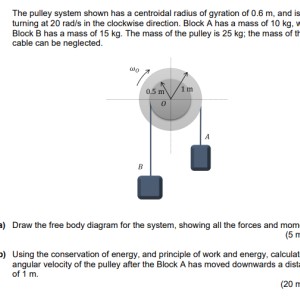
Pulley System
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
5 Attachments
Kav10
-
Thanks alot for this great solution. Can i just query what exactly is going on when you introduce theta Sa and Sb?
-
Sure. When Block A goes down, Block B goes up. The Sa, Sb, ra, and rb shows the ratio of distance moved by each Block to its radius as shown in the picture (ra and rb). The Pulley rotates through the angle teta=Sa/ra=Sb/rb.
-
So this basically accounts for the difference in radius for a and b?
-
also one last question. what does the p on the free body diagram represent.
-
From Newton’s second law of motion, P is the Momentum shown for both Blocks. In this case, P1+T1=Sigma (F)
-
-
To find the U for each Block, you'll need Sa and Sb. However, we don't have Sb and it needs to be calculated. To calculate that, we need to use the radian angle formula I mentioned above, which says the distance moved is proportional to the radius for each Block.
-
sorry however 1 last question. in the line: T1: 8.3827((10x2.2046)^2)=4074.21 What is the 10? I believe you are using 10 in replace of w... however isnt w the initial angular velocity which for this question is 10?
-
It should actually be 20 not 10. You are right, that is a typo. Let me fix it very quick.
-
-
many thanks, i think im being a bit thrown off because you converted to imperial measurement. I am required to complete this in metric. when calculating the torque why are you dividing by 32.2?
-
The 32.2 is to convert to slug unit. See the calculation of Io which results in Slug.ft^2. You can convert these to any measurement system you are comfortable with. Just insert the conversions. One slug is a mass equal to 32.1740 lb (14.59390 kg).
-
Slug unit is very common in rotational motion dynamics.
-
-
my conversions are definitely not coming out correct, by any chance can you complete the Torque section in metric? Using metric measurements i end up with 8.46573w^2, which therefore =3385.292 Nm which is quite different from the result you get in lb.ft
-
Sure. The calculation of the torque section in metric system would be: (1/2)(25)(0.6)^2 * w^2 + (1/2)(10) (w*1)^2 + (1/2)(15) (w*0.5)^2 = 11.375w^2
-
-
Does it make sense?
-
I am going add another section to the solution, doing all calculations in Metric System. Hopefully, that will work better for you. Give me 5 minutes.
-
-
See the last file with metric system calculations. The final answer is the same (slightly changed due to rounding).
-
Hmm im not coming to that same answer. Earlier i find that Io=9kgm^2 So therefore: (.5*9*w^2)+(.5*10*w^2)+(.5*15*0.5(w^2))=13.25*20^2=5300Nm This is effectivly the same numbers as you use however not sure why different outcomes?
-
See the Metric System calculations I just added. The Block A moves 1 meter, but Block B moves 0.5 meter. You have those added incorrectly.
-
-
(1/2)(25)(0.6)^2 * w^2 + (1/2)(10) (w*1)^2 + (1/2)(15) (w*0.5)^2 = 11.375w^2
-
Do you see where you have it wrong?
-
every single way i put this into calculator my output is 13.25w^2. Im pretty confused as to what could possible be different. what parts of mines are incorrectly? Im sure what you have here is the exact same as my forumla above? See these parts of my formula: Block A =(.5*10*w^2) Block B = (.5*15*0.5(w^2)) Pulley = (.5*9*w^2)
-
-
In the Metric System Calculation section, the units shown in front of the final result of each line were still the ft/lb .. So updated those in the last file.
-
i also think that 13.25 seems correct as if you use 11.375 the angular velocity doesnt even change by .01 Rad/s from initial velocity
-
Here: Block B = (.5*15*0.5(w^2)) 0.5 should be inside the parenthesis with w, so it should be (0.5*w)^2. See the the whole formula I added in previous comments, carefully.
-
Do you see it now?
-
-
Yes i now get the same answer as you. Thanks alot. It seems a strange amount of increase.
-
Great! Because of the small numbers for radius and weight, the change in the velocity is not significant.
-
-
Here you state: 'Referring to the FBD of the system shown in part (a), 𝑊𝐴 does positive work and 𝑊𝐵 does negative work.' however i think the FBD actually shows the opposite?
-
No, it is correct. Wa does positive work because that is the one moving down (per question) and since it acts in the same direction of its displacement. Wb does the negative work because it is going the opposite direction.
-
-
when considering Uwa and Uwb why do we not use mgh to find this? Looks as though we didnt miultiply by 9.81 here? will this not effect the final answer?
-
See the unit of the calculation for Uwa and Uwb (kg.m). Work is defined as the product of force and displacement. Work is positive if the force and the movement are in the same direction. If they are opposing, then the work is negative. In the case of a weight, the work is the product of the magnitude of the particle’s weight and its vertical displacement.
-
- answered
- 1027 views
- $13.00
Related Questions
- Sibling Triangle Pairs
- Three questions on the annihilator
- Vector Analysis - Angular Momentum and Acceleration
- Can a plane reflection in 3-space be written as the product of 3 line reflections?
- Find the area of the shaded region
- How do I evaluate and interpret these sets of vectors and their geometric descriptions?
- few questions with Matrices
- Solving for Lambda and Mu
Low bounty!
bounty updated
bounty updated
Low bounty! I can solve it for you if you increase the bounty.
to what value?
$20 should be enough. I can reserve it now and you can pay tip if you cannot increase the bounty.