Help with linear algebra HW. Please show work!
Given that
$$\begin{vmatrix} a & b & c \\ 10d & 10e & 10e \\ g & h & i \end{vmatrix}=7,$$ find the value of
$$\begin{vmatrix} d & e & f \\ a-2g & b-2h & c-2i \\ 5g & 5h & 5i \end{vmatrix}. $$
Hint: Use row operations to transform first to
$$\begin{pmatrix} a & b & c \\ d & e & f \\ g & h& i \end{pmatrix}, $$ then continue to get the ending matrix, keeping track of how your operations change the determinant
Commander96
12
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
Daniel90
443
-
Let me know if you have any questions.
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1057 views
- $2.00
Related Questions
- Frontal solver by Bruce Irons? Am I using the right Algorithm here?
- Problem Help - Matrix/Markov
- Determine values of some constant which equate linear operators whose linear transformation is through a different basis of the same vector space.
- Determinant and Inverse of a predefined matrix. The question and bounty are updated.
- Find the null space of the matrix $\begin{pmatrix} 1 & 2 & -1 \\ 3 & -3 & 1 \end{pmatrix}$
- Question on Subspaces
- Find the values of x
- Consider the matrix, calculate a basis of the null space and column space
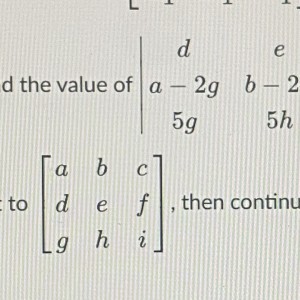
It's hard to read the formulas in your question. Why don't you post a picture of the question?
Didn’t realize I could do that. I just uploaded a picture.
I revised your question. The main change was that I used "pmatrix" in the LaTeX code.
And also vmatrix!