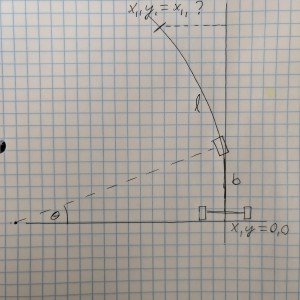
How can I find steering angle if the only information I have is arc length, vehicle length, and how far my vehicle is off course?

Lets say I have a vehicle that has a bad alignment.  I want to know the angle I need to turn the steering in order to drive a straight line.  I can send the vehicle forward a known distance (l),  I know the vehicle length (b), and I know how far it ends up off course at the end of it's path (x).  I do not have the radius or angle of the arc.  How can I find the steering offset (see attached photo)?

What I've tried:
I was able to find the steering angle in terms of x2,y2 by using an offset circle:

$$\left(x-\left(\frac{b}{\sin\theta}\right)\right)^2 + y^2 = \left(\frac{b}{\sin\theta}\right)^2$$

Then solving for $\theta$:

$$\theta = \operatorname{arcsin}\left(\frac{2bx}{x^2+y^2}\right)$$


BUT, I don't know $y$

Geometry Polar Coordinates
Bcherb2 Bcherb2
7
Matchmaticians How can I find steering angle if the only information I have is arc length, vehicle length, and how far my vehicle is off course? File #1 File #1 (jpg)
Report

Answer

Answers can only be viewed under the following conditions:
  1. The questioner was satisfied with and accepted the answer, or
  2. The answer was evaluated as being 100% correct by the judge.
View the answer

1 Attachment

Erdos Erdos
4.7K
  • Bcherb2 Bcherb2
    0

    I do have a question. I am using Excel's solver to find r by iterating x. I entered values of L=50m, B=0.9m, and iterated until x converged on 0.3m. Doing this I get a radius of around 1m. If I plug the same numbers in the equation in my problem statement, I get a radius over 4000m. Any ideas?

  • Erdos Erdos
    0

    The newton's algorithm will converge to r and not x. Make sure you are not confusing r with x. If you run the Newton's algorithm, it should converge to r and not x. Double check and let me know.

  • Erdos Erdos
    0

    There are algorithms to find roots of a nonlinear function. You may also use the intermediate value theorem. See http://www.sosmath.com/calculus/limcon/limcon07/limcon07.html

  • Bcherb2 Bcherb2
    0

    Nice, that worked! I actually had found r-rcos(l/r)=x, but dismissed it because I did not understand how/why I needed to find the roots as you just described. Thank you so much.

The answer is accepted.
Join Matchmaticians Affiliate Marketing Program to earn up to a 50% commission on every question that your affiliated users ask or answer.