Please ignore, I have managed to solve the question (Length of finitely generated module over $0$-dimensional Gorenstein local ring)
Please see attached images: Can someone slowly walk me through the details of the proof of Lemma 4.1 using basic commutative algebraic arguments and definitions?
1) Why $R[m]≅k$? (where $k$ is the residue field of $R$)
2) I know length is additive on direct sums, but how is the RHS of the inequality additive as well, since it is a product?
3) Why does the inequality coincide when $R$ is the module over itself?
4) How does $R$ being Gorenstein of dimension $0$ imply that $R$ is the only indecomposable injective module, and why is its injective hull free as a result?
5) Why $M \subseteq \mathfrak{m}F$?
6) Why does $M=0$ imply the desired result?
Jbuck
152
Join Matchmaticians Affiliate Marketing
Program to earn up to 50% commission on every question your affiliated users ask or answer.
- closed
- 364 views
- $60.00
Related Questions
- Differentiate $f(x)=\int_{\sqrt{x}}^{\arcsin x} \ln\theta d \theta$
- Reverse this equation/function (2d to isometric)
- Multiplying Polynomials
- Linear Algebra - Matrices (Multiple Choice Question) (1st Year College)
- Algebra Question 3
- Attempting to make a formula/algorithm based on weighted averages to find how much equipment we need to maintain.
- Trying to solve this system of simultaneous equations. A solution with work shown would be appreciated.
- Algebra Word Problem 3
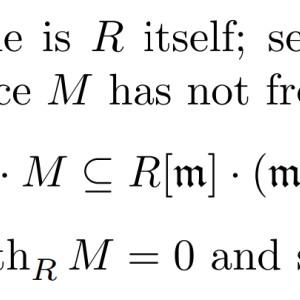
I might be able to give it a look next week, if you extend the deadline. This week I'm on a work trip unfortunately.
Yeah sure, I'm gonna extend by 1 more week, thanks!
Cool, I'll give it a look next Monday, I hope I can get sense of it!
Hey sorry, this week is being bad for me, not a lot of time to spare. I'll still try to check this problem out in the next few days, but I'm not optimistic about actually managing to. Apologies, it's just a very busy period.
That's alright, no worries. I can extend the deadline a bit if you want, but there's absolutely no problem
Hello, I took another look at this question and was able to figure out most of the details myself, so there's no need for you to concern about this. Thanks anyway!
Ok cool, I'm glad you made it!