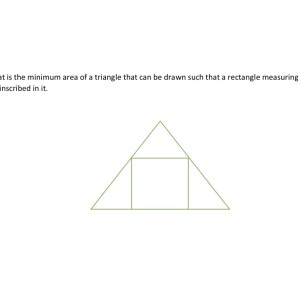
Two calculus questions
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
 Martin
Martin
1.7K
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1319 views
- $13.00
Related Questions
- Find the average of $f(x)=\sin x$ on $[0, \pi]$.
- Exercise 4.33 from Spivak's Calculus on Manifolds.
- Reduction formulae
- What is this question asking and how do you solve it?
- Volume of solid of revolution
- Use Rouche’s Theorem to show that all roots of $z ^6 + (1 + i)z + 1 = 0$ lines inside the annulus $ \frac{1}{2} \leq |z| \leq \frac{5}{4}$
- Help with differentating business caluclus problem.
- Calculus 1