Rolling dice statistics, probability of rolling a straight
How do I correctly set up an equation to solve for the probability of rolling a straight of X amount. First with 5, then 10 then 15 dice and so on. See image.
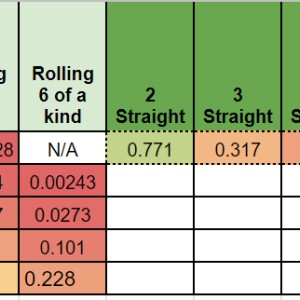
So for example: (6 sided die) I would roll 10 dice all at once, order does not matter. What is the probability I would get at least one straight of 3. Straight of 3 meaning a set of one of these numbers 123 or 234 or 345 or 456.
Edit (rephrasing example question):
What is the probability of rolling 1,2,3 or 2,3,4 or 3,4,5 or 4,5,6 out of 10 dice?
I am making a statistics chart that I can pull data from when making cards for a board game. If this can be done in excel that would be helpful too. I am guessing this is a one and done scenario, so I am not too focus on retaining the knowledge.
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
-
I don't believe it is correct. As 'n' increases the probability of success should too. It is actually the reverse. If you roll 10 dice we get a probably of 0.43 success rate. If you roll 20 dice the success rate is .077. Wouldn't you have better chances of seeing at least 1 straight of 3 as 'n' increases? Or did I interpret it wrong?
-
you are doing something wrong. P_{Failure} is clearly a decreasing function. So 1-P_{Failure} is increasing in n.
- answered
- 1590 views
- $10.00
Related Questions
- Standard Error , P-value
- Expected Value of the Product of Frequencies for a Triangular Die Rolled 15 Times
- Let $X$ be a single observation from the density $f(x) = (2θx + 1 − θ)I[0,1](x)$ with $−1≤ θ ≤ 1$. Find the most powerful test of size $α$ and its power
- Populace Model
- Probability maximum value of samples from different distributions
- Quantitative reasoning
- In each of the situations, state whether the indicated model can be regarded as a Generalized Linear Model (GLM) and give reasons for your answer.
- Critique my null and alternative hypothesis (beginner)


The bounty is low!
What do you believe a fair amount for this would be?
Your example is not clear
Well, it would take at least 30 minutes to write a good solution. Offer whatever you think is a fair bounty for a skilled professional to work for half hour on your problem.
So you roll n die at the same time and you want to compute the probability of say rolling at least one 1, one 2, and one 3 so you have a 123, and you don't care what happens for the remaining (n-3) die?
I will just leave it at $10 for the 4 days and see if its worth anyone's time. Any higher and Chegg is a better route.
Philip, Yes but it can also can be one 2, one 3, one 4 ( 234) or one 3, one 4, one 5 (345) and finally (456). Say I roll 10 dice: 1,1,1,1,2,2,4,4,5,5 = this is a fail, because there is no sequence of 3 (straight of 3). Say I roll again: 1,1,2,2,3,3,4,5,6,6= success, because of multiple sequences of 3. So what is the probability of a success if I roll ten dice. Hope that helps