Explain parameter elimination for complex curves v2
Since I did not get sufficient asnwer I will better ask once again.
I'm reading Stewart's Calculus and in "Calculus with Parametric Curves" he shows the formula which comes from the Chain rule:
$\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}$
But what I don't understand is that for some complex curves for example:
$x = 2\sin\left(1+3t\right), y = 2t^{3}$
If I try to retreive y(x) I will get
$y\ =\ 2\left(\frac{\arcsin\left(\frac{x}{2}\right)-1}{3}\right)^{3}$
Which will represent only small part of the parametric curve(graph).
And only for some small range of t $\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}$. For example when t = 1, $y(x)$ is not defined.
If we take a look into graph of parametric equation it has complex shape and many negative derivatives(negative angles of tangent lines). But y(x) is just a small part of the graph of parametric equation, and it doesn’t have those negative derivatives(angles of tangent lines), since it grows from left to right.
As far as I understand when I represent t as function of x t(x) = $\frac{\arcsin\left(\frac{x}{2}\right)-1}{3}$, the domain of t(x) is [-2;2] and the range is [-pi/6-1/3;pi/6-1/3], and when I substitue t into y(t) to get y(x) this y(x) won't cover those values of t which are out of range, isn't it?
Additionally added the screenshot, on which we can see both parametric equation and y(x). For example when t = 1, derivative of parametric equation is negative (at point (~-1.51,2)). But f(x) doesn not even cover this point, how can it calculate the same derivative value, as all it's deriavtives going to be non-negative?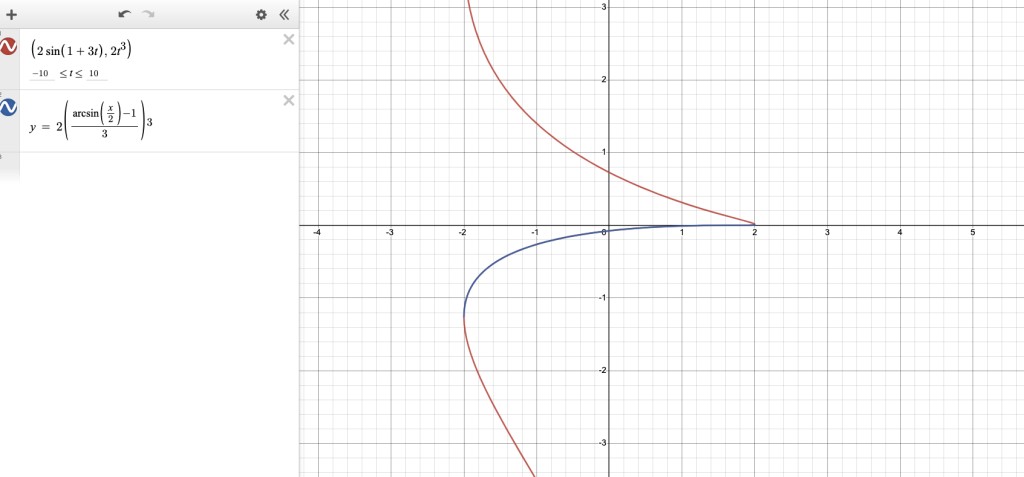
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
1 Attachment
 Mathe
Mathe
-
Mathe, ok, I like that, so did I understand correctly that each complex curve which doesn't pass vertical line test will have multiple y(x), describing it?
-
Yes, if a curve doesn't pass the vertical line, it means it has to be described by multiple y(x) expressions.
-
-
And please let me know if such price is ok for such question, or I have to pay more for the future questions?
-
Since this is a follow up question, a $5 tip would be ok. Separate questions would warrant a different bounty or higher tips.
-
- answered
- 1163 views
- $15.00
Related Questions
- (a) Find the coordinates (x,y) which will make the rectangular area A = xy a maximum. (b) What is the value of the maximum area?
- Integration
- Fermat's method of calculus
- Calculus Questions
- Proof of P = Fv.
- Need help with finding equation of the plane containing the line and point. Given the symmetric equation.
- calculus question
- Integrate $\int \frac{1}{x^2+x+1}dx$
