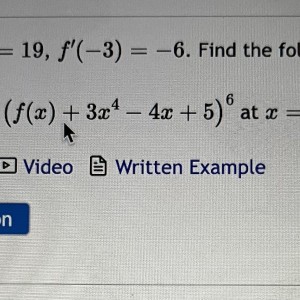
Derivatives again. Thank you!
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
574
-
Both were wrong. I get one more try
-
A minus sign was missing in the final answer. Please try again. It should work now.
-
-
It didn’t work. The answer was 6(19+260)^5(-6-328). I ran out of fund, I’ll try to redo a different one on my own
-
My answer is the same as 6(19+260)^5(-6-328). Probably it is did not accept it because of the format of the answer. 6(19+260)^5(-6-328)=6(279)^5(-334), same as my answer.
-
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1264 views
- $3.00
Related Questions
- Evluate $\int_{|z|=3}\frac{1}{z^5(z^2+z+1)}\ dz$
- Function Invertibility/Inverse & Calculus, One question. Early Uni/College level
- Finding absolute and relative extrema given an equation.
- A rectangular garden plot is to be fenced off along the property line.
- Use Stokes's Theorem to evaluate $\iint_S ( ∇ × F ) ⋅ d S$ on the given surface
- Does $\lim_{n \rightarrow \infty} \frac{2^{n^2}}{n!}$ exist?
- Derivatives
- Business Calculus. Finding the deriviative.