Urgency Can you help me Check these Applications of deritive.
These are the Topics encoutnered in this questions:
05.01 Mean Value and Extreme Value Theorems
05.02 Determining Function Behavior and the First Derivative Test
05.03 Using the Candidates Test to Determine Absolute Extrema
05.04 Determining Concavity of Functions and the Second Derivative Test
05.06 Connecting Graphs of Functions and Their Derivatives
05.07 Optimization Problems
05.08 Exploring Behaviors of Implicit Relations
GOAL: Answer the following question the fastest as possible and accurately so I can compare with my answers
Question 1
(05.05 HC)
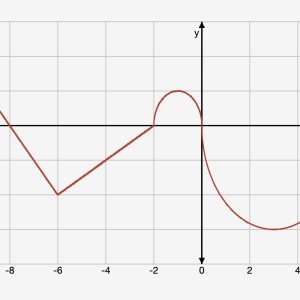
(picture attached) Let h be a continuous function over the interval [−10, 6] with derivative given by h ′ consisting of two line segments and two semicircles, as shown in the graph.
Part A: For what intervals is the graph of h increasing? Decreasing? Justify your answer. (10 points)
Part B: For what value(s) of x does h have relative extrema? Justify your answer. (5 points)
Part C: For what intervals is the graph of h concave up? Concave down? Justify your answer. (10 points)
Part D: For what value(s) of x does h have a point of inflection? Justify your answer. (5 points)
Question 2
(05.08 HC)
[Optimization] A cone will be inscribed in a sphere of radius 9 in.
Part A: Find the exact dimensions of the cone of largest volume that will fit inside the sphere. (20 points)
Part B: Find the maximum volume cone to the nearest tenth. (20 points)
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
 Kav10
Kav10
- answered
- 1089 views
- $32.00