Probability that the distance between two points on the sides of a square is larger than the length of the sides
Two points lie at random position on the border of a square of side length $L$. What is the probability that the distance $D$ between them is larger than $L$?
Plese see the attached image below. I need a detailed mathematical proof. 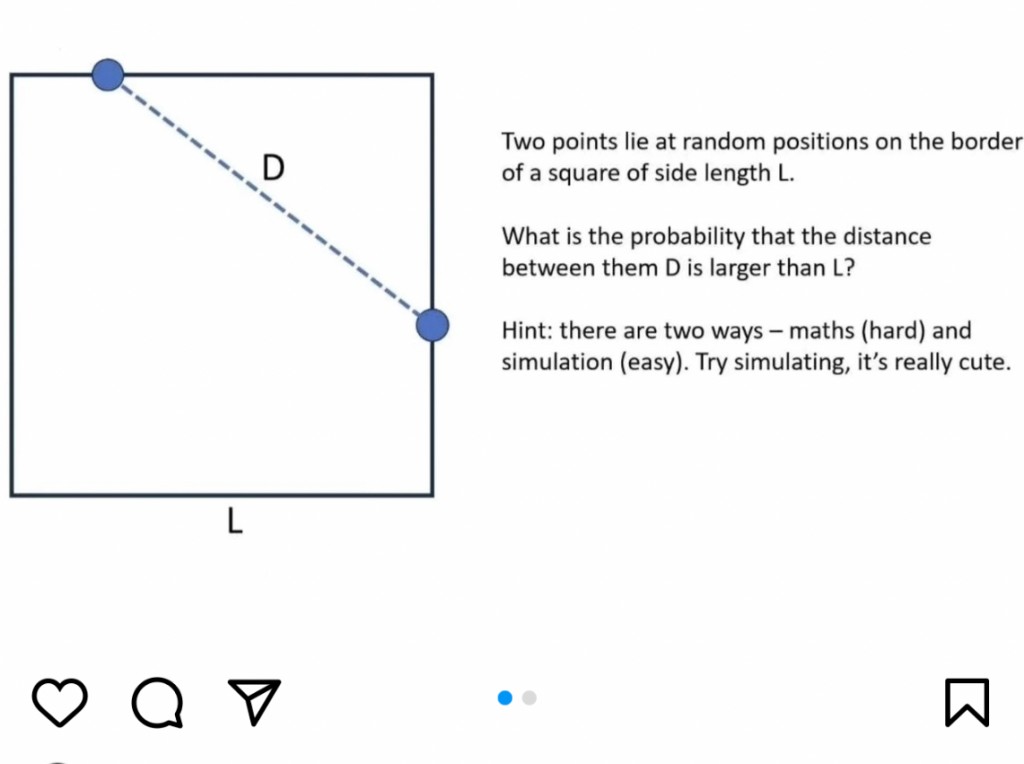
Answer
We consider three cases:
Case I. The two points lie on the same side ($E_1$). Then $P(D\geq L)=0.$
Case II. The two points lie on opposite sides ($E_2$). Then $P(D\geq L)=1.$
Case III. The two points line on adjacent sides ($E_3$).
Lets first calculate the probability of each of these three cases. Let the first point $A$ land on one the 4 sides first. Since all four sides are identical, this could happen in only one way. Then
For Case I to happen, the second point B should land on the same side as $A$. Thus $P(E_1)=\frac{1}{4}$.
For Case II to happen, the second point B should land on the opposite side of $A$. Thus $P(E_2)=\frac{1}{4}$.
For Case III to happen, the second point B should land on the two adjacent sides of $A$. Thus $P(E_3)=\frac{2}{4}$.
Now suppose the two points $A$ and $B$ lie on two adjacent sides. Let $x$ be the distance of $A$ from the corner between the two points, and $y$ be the distance from the point $B$ to the corner. We assume that $x$ and $y$ are both uniformly distributed, i.e. the probability density distribution of $x$ and $y$ are $f_x(x)=\frac{1}{L}, x\in (0,L)$ and $f_y(y)=\frac{1}{L}, y\in (0,L).$ Also $x$ and $y$ are independent. Hence
\[P(D=x^2+y^2\leq L^2)=P(y \leq \sqrt{L^2-x^2})\]
\[=\int_0^{L}\int_0^{\sqrt{L^2-x^2}}\frac{1}{L} \cdot \frac{1}{L} dy dx\]
\[=\frac{1}{L^2} \int_0^{L}\sqrt{L^2-x^2} dx=\frac{1}{L^2}\ \frac{\pi L^2}{4}=\frac{\pi}{4}.\]
Hence $P(D> L)=1-\frac{\pi}{4}.$ Therefore,
\[P[D>L]= P(E_1) P( D>L | E_1)\]
\[+P(E_2) P(D>L | E_2)+P(E_3) P(D>L | E_3)\]
\[=\frac{1}{4} \cdot 0+\frac{1}{4}\cdot 1+\frac{2}{4} \cdot (1-\frac{\pi}{4})\]
\[=\frac{3}{4}-\frac{\pi}{8}\approx 35.73\%.\]
In the above notation $P( D>L | E_1)$ means probability of $D> L$ given that case I has happned. Similarly $P(D>L | E_2)$ means that probability of $D> L$ given that case II has happned, etc.
-
Thank you so much.
- answered
- 4430 views
- $20.00
Related Questions
- Statistics tasks
- Times series Analys
- Introductory statistics, probability (standard distribution, binomial distribution)
- Determine formula to calculate the radii of a unique ellipsoid from coordinates of non-coplanar locii on its surface, and without knowing its center or rotation angles.
- Car accidents and the Poisson distribution
- How to determine which predictor (in multiple linear regression) has the largest effect on the response? Should I be using any statistical test?
- Figure 1 shows two points A and B with a straight line drawn through them.
- Geometry Problem about Hole Placement on PVC Pipe

