Confusing Bonus Question
Do you have any idea what this means and how to solve it? Thanks!2 Answers
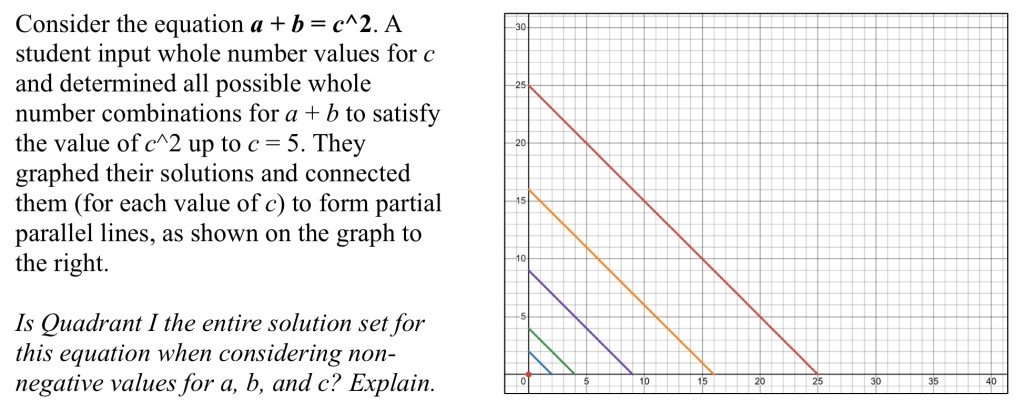
Yes, Quadrant I provides the entire solution set for this question. Indeed for any given $c$, if we let $x=a$ and $y=b$, then $a+b=c^2$, translates to
\[x+y=c^2 \Rightarrow y=-x+c^2\]
which is a line with slope $m=-1$, and $x$-intercept and $y$-intercept are both $c^2$.
For example for $c=5$ you get
\[y=-x+25\]
which is the question of the red line in the image.
Savionf
-
I think the solutions of the given equation are triples (a,b,c), not pairs (a,b). So the solution set is not Quadrant I, but a 2-dimensional submanifold of $\R^3$, the segment from (c², 0, c) to (0, c², c), for each allowed value of c.
According to the problem statement, I would say that the solutions to the equation are triples $(a,b,c)$, rather than pairs $(a,b)$. So the solution set is $\{ (a, c²-a, c) ~;~ 0 \le a \le c², c \in \R_+ \} = \{ (x, y, \sqrt{x+y}) ~;~ x,y\in \R_+ \} $.
This is a subset of $\R_+^3\subset \R^3$, not of $\R²$, although it is two-dimensional: For each allowed value of $c\in\R_+$, for example $a$ can be chosen in the interval $[0, c²]$ and b is determined as $c²-a$ (or reciprocally). That is, the solutions form the segment (straight line) from $(0, c², c)$ to $(c²,0,c)$. Glueing all these subsets together yields "the first quadrant raised to the height" $z = \sqrt{x+y}$ above a point $(x,y,0)$ on the $\{ z = 0 \}$ plane.
According to the problem statement, it was a choice of the student to consider $c$ as a given parameter for drawing some solutions - that is, the orthogonal projection of these particular solutions $(a,b,c)$ on $\R^2\times\{0\}$, "the first two coordinates" $(a,b)$. But otherwise there is no reason for considering $c$ as a parameter rather than a component of the solution $(a,b,c)$ of the given equation.
M F H
- 2 Answers
- 282 views
- Pro Bono
Related Questions
- Double absolute value equations.
- What can we say about the transformation ?
- Find $a,b,c$ so that $\begin{bmatrix} 0 & 1& 0 \\ 0 & 0 & 1\\ a & b & c \end{bmatrix} $ has the characteristic polynomial $-\lambda^3+4\lambda^2+5\lambda+6=0$
- Domain question
- Does $\lim_{(x,y)\rightarrow (0,0)}\frac{(x^2-y^2) \cos (x+y)}{x^2+y^2}$ exists?
- Algebra Word Problem #1
- If both $n$ and $\sqrt{n^2+204n}$ are positive integers, find the maximum value of $𝑛$.
- Trying to solve this system of simultaneous equations. A solution with work shown would be appreciated.
