What Are The Odds ?
You are going to spin a perfectly balanced pointer on a wheel with five spaces numbered 1 through 5.
(See attachment)
You are going to spin for five sets of fifty.
The first set you are going to spin 50 times in an attempt to land on space #1. The second set you spin 50 times trying to land on space #2. Third set- 50 times to land on #3. Fourth set- 50 times to land on #4. And finally, you spin 50 times in an attempt to land on space #5.
In each set, you land on multiples of each number EXCEPT for the number you are attempting to land on. You never land on the target number in either set.
What are the odds of this happening?
I will gladly up the bounty if your credentials merit it. I have already posed this question to ChatGPT. I just need an answer from a human math expert.
 Baddcatt
Baddcatt
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
-
I like your answer, Schwartstack. And I'm impressed with your credentials. The bounty is yours. Thank you.
- answered
- 1316 views
- $25.00
Related Questions
- Random Walk on Cube
- Estimating the Suit with 12 Cards: MLE and Confidence Intervals in a Figgie Starting Hand
- Find Mean, Variance, and Distribution of Recursively Defined Sequence of Random Variables
- Bivariate Normality questions
- How do you calculate per 1,000? And how do you compensate for additional variables?
- Drawing a random number with chance of redrawing a second time. Best strategy that will never lose long term?
- Central Limit Theorem question
- Prove that the following sequences monotnically decrease and increase correspondingly. Since they are bounded, find the limit.
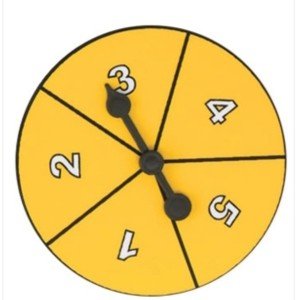

Can you clarify this: In each set, you land on multiples of each number EXCEPT for the number you are aattempting to land on?
Yes. Typo on attempting. I have now corrected it. But in the scenario, in each set of 50 spins, you never land on the target number but instead you land on the other spaces different number of times.