Write a Proof
Hey! I would like assistance in writing a proof (step by step) to show the distance between a vertex and a co-vertex is the SAME as the distance between the center and a focus for hyperbolas. In simpler terms, why is x=y? I would really appreciate an illustration to go with the answer of some sort, and will pay however much is needed for the best possible answer.
Good Luck!
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
 Aman R
Aman R
649
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1652 views
- $15.00
Related Questions
- Find all values of x... (Infinite Sums)
- A bicycle with 18in diameter wheels has its gears set so that the chain has a 6 in. Radius on the front sprocket and 4 in radius on the rear sprocket. The cyclist pedals at 180 rpm.
- Find the area of the shaded region
- Calculus / imaginary numbers and S^2
- Compute $\lim_{x \rightarrow 0} \frac{1-\arctan (\sin(x)+1)}{e^{x}-1}$
- Work problem involving pumping water from tank
- Profit maximizing with cost and price functions
- Obtaining the absolute velocity of a moving train based on angle of raindrops with respect to vertical axis
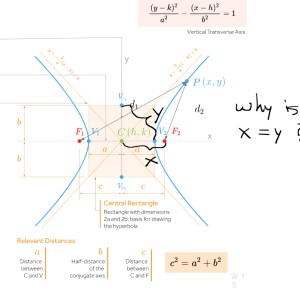

Can you increase it :) I will show a proof ! Thanks
Ok!
Sorry it looks like I cant add to a question's total bounty if it has already been accepted to be answered.
thank you so much!!
Welcome, it would be great if you accept the answer if you are satisfied. Thanks
Oops! My bad first time using the site
thank you so much