Growth of Functions
Need solutions for the following questions with step by step work shown
(a)
Let $f(x) = x^2 +x + 15$ and $g(x) = x^2 log(x) + 10$. Prove that f(x) is O(g(x)) by:
1. Providing witnesses C and k and
2. Proving that the inequality holds for the value you choose in 1.
(b)
Let $f(x) = x^5 + 10$ and $g(x) = x^5 + x + 10$
1. Prove that $f is O(g)$
2. Prove that $f is Ω(g)$
3. Given parts a and b, what other relationship can you show about f and g?
Jack Smith
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
1 Attachment
Erdos
-
Leave a comment if you need any clarifications.
-
thanks phil. Can you please label parts 1 and 2 of (a) and also if possible solve the question with some other relatively lower value for C (say 3,4,5,17) .
-
Will really appreciate if you'd write back:)
-
What I have written for (a) answers part 2 of the question. The last line answers part 1, i.e. k=1 and C=e^2.
-
So the answer for part 1 is k=1 and C=e^2.
-
In this kind of questions values of C does not matter, you just need to show that for some C and K the inequality holds and that's what we have done here.
-
This is actually a homework question for a course I am already on thin ice on. The grader is kinda sadistic and I am pretty sure he won't give me any points unless I solve the first part(C and K) followed by the second (inequality).
-
Please understand my plight and sorry I am coming across as annoying.
-
Sir, the answer for part 1 i: s k=1 and C=e^2. The answer for part 2 is in the file I uploaded. You seem to be overthinking this. Everything is ok, relax and submit your homework.
- answered
- 564 views
- $4.00
Related Questions
- Mathematically determine the length and width of board required to make a box
- Graph theory question on Euler circuit, Euler path, Hamilton circuit, and Hamilton path
- Find H $\langle H \rangle=P+\frac{1}{AD} \sum_{i=0}^{D} ( \sum_{j=0}^{A} ((j-i)Step(j-i)))$
- Beginner Question on Integral Calculus
- Domain question
- Sinusoidal function question help
- Probability of making a full house in a poker hand
- In how many different ways $n$ persons can seat around a round table?
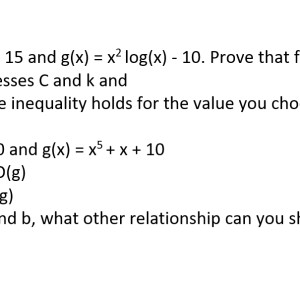
Please provide full answers, and please solve them in a way that a someone who semi-understands (me) can comprehend and study it in the future
That's what Matchmaticins actually expects from the answerers. All solutions should be written so someone with basic background can understand. I wrote a very detailed solution, but let me know if you need any clarification.