Set Theory Question Help
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
 Aman R
Aman R
649
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1400 views
- $17.00
Related Questions
- In how many different ways $n$ persons can seat around a round table?
- Determine formula to calculate the radii of a unique ellipsoid from coordinates of non-coplanar locii on its surface, and without knowing its center or rotation angles.
- Find the generating function
- Why does this spatial discretization with n intervals have a position of (n-1)/n for each interval?
- Irrational Number
- Find the chromatic number of Kn, Kn,m, Cn.
- Logic Question ¬¬𝐴→𝐴
- Count the number of decks of cards, where no king is on top of the ace of the same suit.
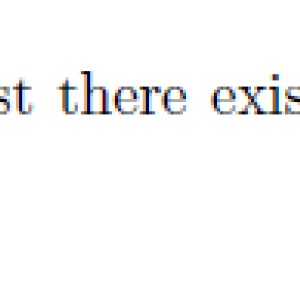

I believe bounty should be larger for an advanced question.
I have a proof using the axiom of choice, is that ok? Also, I agree the bounty should be larger for this question.
Yeah, I guess that should be fine. What's an appropriate bounty for this question?
Maybe $16