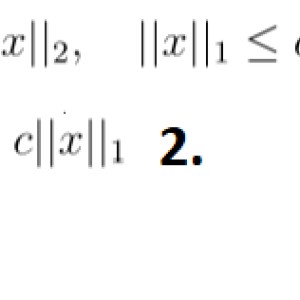Help with Norms
I need help with two exercises:
1. I need to find (with poof) the constants c_1, c_2 > 0, so that the 2 statements / formulas in the first part of the image are true for $\forall x\in\mathbb{R}^n$ :
2. I need to find a constant c > 0, so that for all $x\in \mathbb{R}^n$ the second part of th image (2.) is true and for some $x\neq 0$ , the two are equal.
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
1.7K
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1141 views
- $19.74
Related Questions
- Find $\int x \sqrt{1-x}dx$
- 35 min question
- Compute $\lim_{n \rightarrow \infty} \ln \frac{n!}{n^n}$
- Use the equation to show the maximum, minimum, and minimum in the future.
- [Help Application of Integration]Question
- Calculating Driveway Gravel Area and Optimizing Cardboard Box Volume
- Let $ X = x i+ y j+z k$, and $r=||X||$. Prove that $\nabla (\frac{1}{r})=-\frac{X}{r^3}.$
- Is my answer correct?