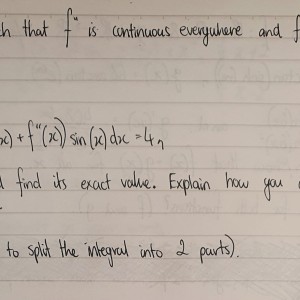Early uni/college Calculus (one question)
Attatched question pic below. Answer doesn't have to be long, can be somewhat middle of short n long, but precise or straight to the point with the working. Thank you.
 Limahun
Limahun
18
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
 Dynkin
Dynkin
779
-
comment: upon reading the answer again I note that I made a miscalculation. In the third equation one should get f(\pi) * (1) - f(0) * (-1) instead of f(\pi) *(-1) - f(0)*(-1) - as cos(\pi)=-1 not 1. This should then enter into the second to last equation where you get 4 = f(0) + 9, the solution then becomes f(0)= 4-9 = -5.
-
Unfortunately it is not possible to edit answers once they are submitted, which is why I must put the correction in a comment instead.
-
Yes that is all good, thanks so much for your help!
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1393 views
- $3.00
Related Questions
- Extremal values/asymptotes
- Calculus Help
- Evaluate the line intergral $\int_C (2x^3-y^3)dx+(x^3+y^3)dy$, and verify the Green's theorem
- Studying the graph of this function
- Find the amount of work needed to pump water out of full spherical tank
- Calculus - 2nd order differential equations and partial derivatives
- Line Integral
- Derivative of $\int_{\sin x}^{x^2} \cos (t)dt$