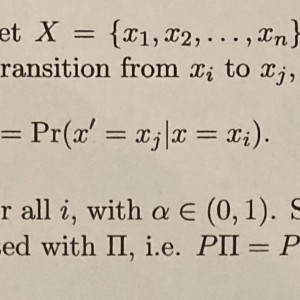Markov Process Problem
Any help is greatly appreciated. I'm completely lost.
Answer
We know that $P=P \Pi $. Also note that $P$ is a $1\times n$ matrix aka a row vector. So the k-th component of $P$ is $P$ times the k-th column of $\Pi$ :
$$ p_k =\sum _{i=1}^n p_i \pi _{ik} = \sum _{i=1}^n p_i \alpha = \alpha \sum _{i=1}^n p_i =\alpha 1=\alpha $$ since $P$ is a probability distribution and the sum of its components is one.
The interpretation is that if the probability of reaching the state $x_k$ from any state is the constant $\alpha$, then in the stationery distribution, which is the same as the probability distribution in the long run, the probability of being in the state $x_k$ is also $\alpha$.
 Martin
Martin
1.7K
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1471 views
- $24.00
Related Questions
- Logic Question 𝐴→(𝐵→𝐶),𝐴→𝐵,𝐴⊢𝐶
- Combinatorics/counting: How many configurations are possible for m differenct objects in n boxes of unlimited occupany (m<n)
- [Discrete Mathematics] Algorithm and Pseudocode - Write an algorithm to find the roots of a quadratic equation ax2 + bx + c = 0. Write Pseudocode of algorithm.
- Discrete Math- Number of factor trees of a graph
- Singular Value Decomposition Example
- Proof by induction the following recursive equation
- Recursive Set
- Probability of making a full house in a poker hand